USP 2022 Matemática - Questões

Uma sequência de números naturais é construída da seguinte forma: seu primeiro termo $t_1$ é escolhido como sendo um número natural qualquer. Se $t_1$ for par, então $t_2=\dfrac{t_1}{2}$ e, se $t_1$ for ímpar, então $t_2=3t_1+1$. Os termos seguintes $t_n$ são obtidos de acordo com essa mesma regra. Por exemplo, se $t_1=3$, então $t_2=10, \ t_3=5, \ t_4=16$ e assim por diante.

Dessa forma, a partir de $t_1 \ \in \ \mathbb{N}$, para cada $n \ \in \mathbb{N}, \ n \geq 2$, a sequência $t_n$ é definida como

$$t_n=\begin{cases} \begin{array}{ll} \dfrac{t_{n-1}}{2}, & \text{se} \ t_{n-1} \ \text{for par} \\ \\ 3t_{n-1}+1, & \text{se} \ t_{n-1} \ \text{for ímpar} \end{array} \end{cases}$$

1. a) Para $t_1 = 22$, determine $t_4$.
   

2. b) Determine todos os possíveis $t_1$ para os quais $t_4 = 10$.
   

3. c) Para $t_1 = 26$, determine $t_{2022}$.
   

Considere o conjunto $C$ de pontos do plano cartesiano da forma $(m, \ n)$ com $m$ e $n$ pertencentes a $\{3,\ 4, \ 5, \ 6, \ 7, \ 8, \ 9\}$.

Note e Adote:

Uma fração $\dfrac{m}{n}$ é redutível quando $m$ e $n$ possuem um divisor natural em comum, além do $1$.

1. a) Apresente todos os pontos $(m, \ n)$ de $C$ para os quais o produto $m \cdot n$ é maior do que $60$.
   

2. b) Sorteando-se um ponto $(m, \ n)$ de $C$, com iguais probabilidades para todos os pontos, qual é a probabilidade de que a fração $\dfrac{m}{n}$ seja redutível?
   

3. c) Sorteando-se, com iguais probabilidades, dois pontos distintos de $C$, qual é a probabilidade de que a distância entre eles seja igual a $\sqrt{13}$?
   

O gráfico mostra dados coletados na cidade do Rio de Janeiro, entre fevereiro e abril de 2020, período que inclui o início das medidas de restrição de circulação na cidade por causa da pandemia de COVID-19. Para cada dia, representado por um símbolo no gráfico, foram coletadas duas grandezas: uma média da energia de vibração sísmica durante o dia (na abscissa) e o índice $F$ (na ordenada), que é a fração de pessoas que saiu de casa alguma vez naquele dia. A energia sísmica média foi medida em $(\text{nm/s})^2$ na faixa de frequências que tem causas humanas. Os triângulos representam domingos e feriados; os quadrados referem-se aos sábados; e os círculos correspondem aos dias úteis da semana. Para cada um desses subconjuntos de dados, uma reta média foi obtida, expressando a relação aproximada entre as duas grandezas medidas.

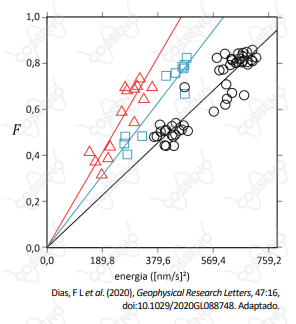
Dias, F L et al. (2020), Geophysical Research Letters, 47:16, doi:10.1029/2020GL088748. Adaptado.

Sobre o estudo descrito, o que é possível inferir a partir dos dados apresentados?

Considere, no plano cartesiano, a circunferência com centro no ponto $(0 , \ 3)$ e com raio $2$ e, para cada $a \ \in \mathbb{R}, \ a \ne 0$, a parábola cuja equação é $y=ax^2+1$.

1. a) Para $a=-1$, encontre o ponto comum entre a circunferência e a parábola.
   

2. b) Para $a=1$, apresente $3$ pontos em comum entre a circunferência e a parábola.
   

3. c) Encontre todos os valores de $a$ para os quais a circunferência e a parábola possuam exatamente $3$ pontos em comum.
   

Uma empresa distribuidora de alimentos tem latas de ervilha $(E)$ e latas de milho $(M)$, em dois pesos, $1 \ \text{kg}$ e $2 \ \text{kg}$, totalizando $4$ (quatro) tipos de latas: $E_1$ e $E_2$ (ervilha, em pesos de $1 \ \text{kg}$ e $2 \ \text{kg}$, respectivamente) e $M_1$ e $M_2$ (milho, em pesos de $1 \ \text{kg}$ e $2 \ \text{kg}$, respectivamente). Essas latas são agrupadas em pacotes para envio aos comerciantes. Dois pacotes de latas são considerados iguais se contiverem a mesma quantidade de latas de cada tipo, independentemente da maneira como são organizadas no pacote.

1. a) Quantos pacotes diferentes pesando, cada um, exatamente $200 \ \text{kg}$ (duzentos quilos) podem ser montados usando-se apenas latas dos tipos $E_1$ e $E_2$? Na contagem, deve-se também levar em conta pacotes formados por apenas $1$ tipo dessas latas.
   

2. b) Quantos pacotes diferentes pesando, cada um, exatamente $200 \ \text{kg}$ (duzentos quilos) podem ser montados usando-se apenas latas dos tipos $E_1$, $E_2$ e $M_1$? Na contagem, deve-se também levar em conta pacotes formados por apenas $1$ ou $2$ tipos dessas latas.
   

3. c) Quantos pacotes diferentes pesando, cada um, exatamente $20 \ \text{kg}$ (vinte quilos) podem ser montados usando-se latas dos tipos $E_1$, $E_2$, $M_1$ e $M_2$? Na contagem, deve-se também levar em conta pacotes formados por apenas $1$, $2$ ou $3$ tipos dessas latas.