USP 2020 Matemática - Questões

Um jogo educativo possui $16$ peças nos formatos: círculo, triângulo, quadrado e estrela, e cada formato é apresentado em $4$ cores: amarelo, branco, laranja e verde. Dois jogadores distribuem entre si quantidades iguais dessas peças, de forma aleatória.

O conjunto de $8$ peças que cada jogador recebe é chamado de coleção.

1. a) Quantas são as possíveis coleções que um jogador pode receber?
   

2. b) Qual é a probabilidade de que os dois jogadores recebam a mesma quantidade de peças amarelas?
   

3. c) A regra do jogo estabelece pontuações para as peças, da seguinte forma: círculo $= 1$ ponto, triângulo $= 2$ pontos, quadrado $= 3$ pontos e estrela $= 4$ pontos. Quantas são as possíveis coleções que valem $26$ pontos ou mais?
   

É dada a função $f: [0, \pi] \ \rightarrow \ \mathbb{R}$ definida por $f(x) = \hspace{2pt}\mathrm{sen}^4\ x + \cos^4\ x$, para todo $x \in [0, \pi]$.

1. a) Apresente três valroes $x \in [0, \pi]$ para os quais $f(x) = 1$.
   

2. b) Determine os valores de $x \in [0, \pi]$ para os quais $f(x) = \dfrac{5}{8}$.
   

3. c) Determine os valores $x \in [0, \pi]$ para os quais $\dfrac{1}{2} f(x) + \dfrac{3}{8} \hspace{2pt}\mathrm{sen}\ (2x) \geq \dfrac{5}{8}$.
   

Resolva os três itens abaixo:

1. a) Considere o conjunto formado pelos números complexos $z$ que cumprem a condição $\mathrm{Re}(z) = \mathrm{Im}(z)$. Cada elemento desse conjunto será objeto da transformação que leva um número complexo em seu conjugado. Represente no plano complexo (ou plano de Argand‐Gauss) da folha de respostas o conjunto resultante após essa transformação.
   

2. b) Determine o lugar geométrico dos pontos $z$ do plano complexo tais que $z \neq -1$ e para os quais $\dfrac{z-1}{z+1}$ é un número imaginário puro.
   

3. c) Determine as partes reais de todos os números complexos $z$ tais que as representações de $z$, $i$ e $1$ no plano complexo sejam vértices de um triângulo equilátero.
   

Para exemplificar probabilidade, um grupo de estudantes fez uma atividade envolvendo química, conforme o procedimento descrito.

Cada estudante recebeu um recipiente contendo $800\ \text{mL}$ de água destilada com algumas gotas do indicador de $pH$ alaranjado de metila e soluções de $HCl$ e $NaOH$ em diversas concentrações.

Cada estudante deveria jogar apenas uma vez dois dados, um amarelo e um vermelho, ambos contendo os números de $1$ a $6$.

• Ao jogar o dado vermelho, o estudante deveria adicionar ao recipiente $100\ \text{mL}$ de solução do ácido clorídrico na concetração $10-n\ \text{mol/L}$, sendo $n$ o número marcado no dado (por exemplo, se saísse o número $1$ no dado, a solução seria de $10-1\ \text{mol/L}$; se saísse $6$, a solução seria de $10-6\ \text{mol/L}$).

• Ao jogar o dado amarelo, o estudante deveria executar o mesmo procedimento, mas substituindo o ácido por $NaOH$, totalizando assim $1,0\ \text{L}$ de solução.

• O estudante deveria observar a cor da solução ao final do experimento.

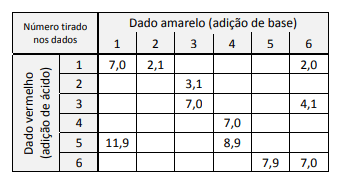
A professora mostrou a tabela com alguns valores de $pH$ resultantes conforme os números tirados nos dados. Ela pediu, então, aos estudantes que utilizassem seus conhecimentos e a tabela para prever em quais combinações de dados a cor final do indicador seria vermelha.

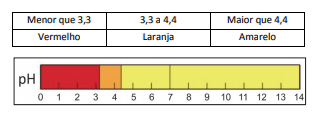
A probabilidade de, após realizar o procedimento descrito, a solução final preparada por um estudante ser vermelha é de:

Carros que saem da cidade $A$ rumo a alguma das cidades turísticas $E$, $F$ e $G$ fazem caminhos diversos, passando por pelo menos uma das cidades $B$, $C$ e $D$, apenas no sentido indicado pelas setas, como mostra a figura.

Os números indicados nas setas são as probabilidades, dentre esses carros, de se ir de uma cidade a outra.

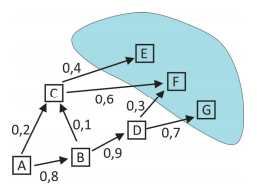
Nesse cenário, a probabilidade de um carro ir de $A$ a $F$ é: