UNICAMP 2022 - Questões

Dados os números reais positivos $a_{1}, a_{2},..., a_{n}$ a média geométrica $M$ destes termos é calculada por:

$$M=\sqrt[n]{a_{1}\cdot a_{2} \cdots a_{n}}$$

A média geométrica de $1, 10, 100, ... , 10^{22}$ é:

Para conter uma certa epidemia viral, uma vacina será aplicada a uma população. Sabe-se que :

- a efetividade de uma vacina pode ser entendida como sendo a porcentagem dos indivíduos vacinados que estarão imunes à doença; e

- para controlar a epidemia, a porcentagem mínima de uma dada população a ser imunizada é dada pela fórmula $I(R_{0})=\dfrac{100\cdot (R_{0}-1)}{R_{0}}$, em que $R_{0}>1$ é um valor associado às características da epidemia.

Assume-se, ainda, que uma eventual imunização somente é adquirida por meio da vacina.

Assuma que $R_{0}=2$. Sabendo que cada uma dada vacina tem $80 \%$ de efetividade, em qual dos intervalos se encontra a porcentagem mínima da população que deve ser vacinada para controlar a pandemia?

Considere a matriz

$$A= \left(\begin{matrix} 1 & k \\ 3 & k^2 \end{matrix} \right)$$

e seja $B=A+A^{T}$, onde $A^{T}$ é a transposta da matriz $A$. Sobre o sistema

$$B \cdot \left( \begin{matrix} x \\ y \end{matrix} \right)= \left( \begin{matrix} 2021 \\ 2022 \end{matrix} \right)$$

é correto afirmar que:

A parábola $y=-x^2 +bx +c$ intercepta o eixo $x$ nos pontos $(p,0)$ e $(q,0)$. Sabe-se que ela intercepta uma única vez cada uma das retas dadas pelas equações $y=2x+1$ e $y=1-\dfrac{x}{2}$. O valor de $p+q$ é:

No dia $23$ de março de $2021$, um navio encalhou no canal de Suez, no Egito. A embarcação tinha $400\ \text{metros}$ de comprimento e $60\ \text{metros}$ de largura. No ponto onde aconteceu o acidente, o canal de Suez não tem mais do que $200\ \text{metros}$ de largura. Abaixo apresentamos uma foto de satélite e uma figura representando a situação. O ângulo $\alpha$ indicado na figura abaixo mede $67,5^{\circ}$.

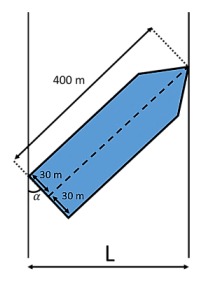
A largura do canal, medida em metros e indicada por $L$ na figura anterior, é:

Dados:

- $\cos\ (2\theta)=2\cos^2\ (\theta)-1$ - $\hspace{2pt}\mathrm{sen}\ (2\theta)=2\hspace{2pt}\mathrm{sen}\ (\theta) \cos\ (\theta)$.