EN 2012 Matemática - Questões

Considere a função real de variável real definida por $f(x)=3x^4-4x^3+5$ . É verdade afirmar que

Os números reais a,b,c,d,f,g,h constituem, nesta ordem, uma progressão aritmética. Se $e^{det\ A}=\displaystyle\lim_{x\rightarrow +\infty}\left(1+\dfrac{2}{y}\right)^{\frac{y}{9}}$, onde $A$ é a matriz $\begin{bmatrix}1 & a & a^2\\ 1 &b &b^2\\1 &d &d^2 \end{bmatrix}$ e $h=\displaystyle\sum_{n=3}^{+\infty}\left(\dfrac{1}{4}\right)^{n}$, então o valor de $(b-2g)$ vale

Considere a função $f(x)=\ln(\text{sec}x+\tan x)+2\sin x$, com $0<x<\dfrac{\pi}{2}$. O resultado de $\int[(f'(x))^2+2-2\cos 2x]dx$ é

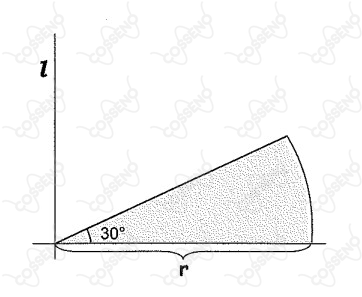
Considere dois cones circulares retos de altura $H$ e raio da base $1\ cm$, de modo que o vértice de cada um deles é o centro da base do outro. O volume comum aos dois cones coincide com o volume do sólido obtido pela rotação do setor circular, sombreado na figura abaixo, em torno do eixo $l$. O valor de $H$ é, em $cm$,

Sejam $A$ e $B$ conjuntos de números reais tais que seus elementos constituem, respectivamente, o domínio da função $f(x)=\ln(2+x+3|x|-|x-1|)$ e a imagem da função $g(x)=-2+\dfrac{\sqrt{2(x+|x-2|)}}{2}$. Pode-se afirmar que