Observe a figura abaixo 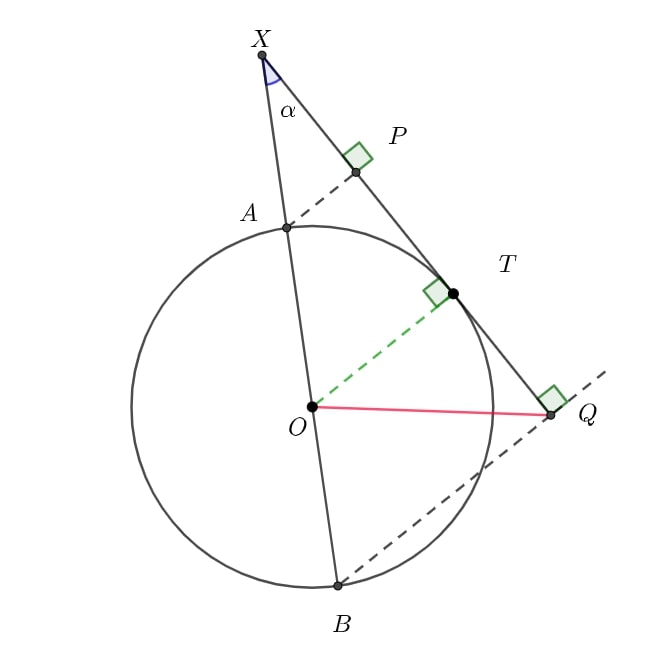Nós queremos calcular justamente o $\alpha$. Primeiramente, note que $\Delta OTQ$ é retângulo, portanto, $$TQ^2 + OT^2 = OQ^2 \Rightarrow TQ^2 + R^2 =\left( \frac{\sqrt{7}R}{2}\right)^2 \Rightarrow TQ = \frac{\sqrt{3}R}{2}$$ Finalmente, pelo Teorema de Tales, uma vez que $\overline{AP}, \overline{OT}, \overline{BQ}$ são paralelos (todos perpendiculares à reta tangente): $$\frac{XQ}{TQ} = \frac{XB}{OB} \Rightarrow \cos{\alpha} = \frac{\sqrt 3}{2} \Rightarrow \alpha = \frac{\pi}{6}$$