Na figura abaixo, o cilindro de volume , contém um gás inicialmente a uma pressão encontra-se conectado, através de uma tubulação dotada de uma válvula (), a um vaso menor de volume , repleto do mesmo gás a uma pressão tal que , onde é a pressão atmosférica local.
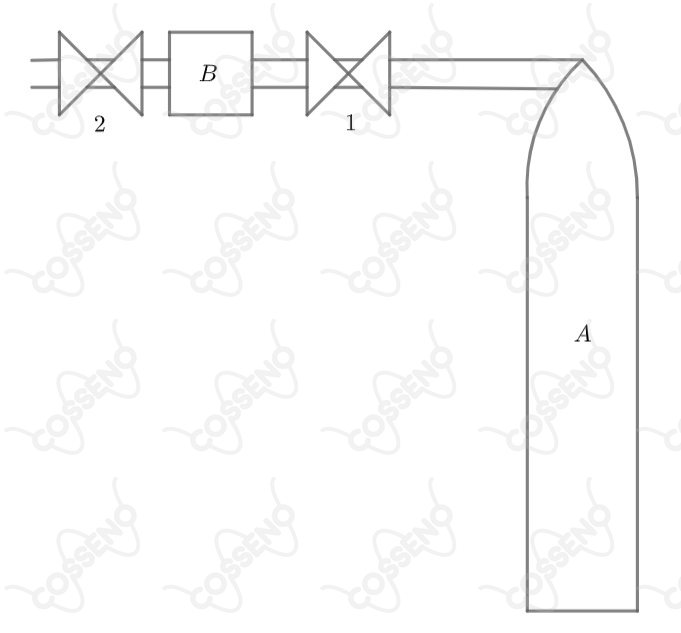
Abre-se a válvula até que a pressão fique equalizada nos dois vasos, após o que, fecha-se esta válvula e abre-se a válvula até que a pressão do vaso menor retorne ao seu valor inicial , completando um ciclo de operação. Sabendo-se que o sistema é mantido a uma temperatura constante , pede-se uma expressão para a pressão do vaso após ciclos.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A ideia aqui é analisar o comportamento matemático da pressão do vaso $A$ entre o estado $k$ e o estado $k+1$, entre um ciclo. Observe que o que faz mudar a pressão em $A$ durante o ciclo é exclusivamente a redistribuição de quantidade de gás.
Seja $p_k$ a pressão em $A$. Temos que $$p_k \cdot V_A = n_k \cdot R \cdot T$$ Em $B$: $$pV_B = n_{retido}RT$$Após abrir a válvula, teremos: $$P_{equilibrio} \cdot (V_A + B_B) = (n_k + n_{retido})RT \Rightarrow P_{equilibrio} = p_k \cdot \dfrac{V_A}{V_A + V_B} + p \cdot \dfrac{V_B}{V_A +V_B} $$Após fecharmos a válvula $1$ a pressão em $A$ será então $$p_{k+1} = P_{equilibrio} = p_k \cdot \dfrac{V_A}{V_A + V_B} + p \cdot \dfrac{V_B}{V_A +V_B}$$Ou seja, em cada ciclo, a pressão é sempre acrescida de um valor constante e multiplicada por um valor constante. Temos uma superposição de uma P.A. e de uma P.G.
P.A.: após $N$ ciclos, $$p_{n} = \dfrac{P_0 \cdot V_A^n}{(V_A + V_B)^n} + \dfrac{p\cdot V_B}{V_A + V_B}\bigg(1 + \dfrac{V_A}{V_A + V_B} + \dfrac{V_A^2}{(V_A+V_B)^2} + \cdots + \dfrac{V_A^{n-1}}{(V_A+V_B)^{n-1}}\bigg)$$ A segunda expressão é a soma de uma P.G. que será dada por $$\dfrac{\bigg(\dfrac{V_A}{V_A+V_B}\bigg)^n - 1}{\dfrac{-V_B}{V_A+V_B}}$$Por fim, a expressão fica $$p_n = \dfrac{P_0 \cdot V_A^n}{(V_A + V_B)^n} + p - p\cdot \bigg(\dfrac{V_A}{V_A+V_B}\bigg)^n \Rightarrow p_n = p + (P_0 - p) \cdot \bigg(\dfrac{V_A}{V_A+V_B}\bigg)^n$$

