USP 2014 Matemática - Questões

Os coeficientes $a$, $b$ e $c$ do polinômio $p\left(x\right)=x^3+a \cdot x^2+b \cdot x+c$ são reais. Sabendo que $-1$ e $1 +\alpha i$, com $\alpha > 0$, são raízes da equação $p\left(x\right)=0$ e que o resto da divisão de $p\left(x\right)$ por $\left(x-1\right)$ é $8$, determine:

($i$ é a unidade imaginária. $i^2=-1$.)

1. a) O valor de $\alpha$;
   

2. b) O quociente de $p\left(x\right)$ por $\left(x+1\right)$.
   

Um recipiente hermeticamente fechado e opaco contém bolas azuis e bolas brancas. As bolas de mesma cor são idênticas entre si e há pelo menos uma de cada cor no recipiente. Na tentativa de descobrir quantas bolas de cada cor estão no recipiente, usou-se uma balança de dois pratos. Verificou-se que o recipiente com as bolas pode ser equilibrado por:

1. I. $16$ bolas brancas idênticas às que estão no recipiente ou
   

2. II. $10$ bolas brancas e $5$ bolas azuis igualmente idênticas às que estão no recipiente ou
   

3. III. $4$ recipientes vazios também idênticos ao que contém as bolas.
   

Sendo $P_A$, $P_B$ e $P_R$, respectivamente, os pesos de uma bola azul, de uma bola branca e do recipiente na mesma unidade de medida, determine

1. a) Os quocientes $\dfrac{P_{A} }{P_{B} }$ e $\dfrac{P_{R} }{P_{B} }$;
   

2. b) O número $n_A$ de bolas azuis e o número $n_B$ de bolas brancas no recipiente.
   

Analise o gráfico abaixo:

RAZÃO ENTRE SEXOS (M:F) DAS PESSOAS COM AIDS, DE ACORDO COM O ANO DE DIAGNÓSTICO - BRASIL 1986 A 2008

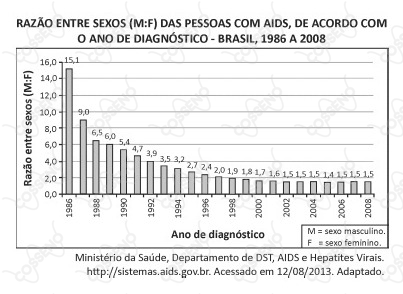
(Ministério da Saúde, Departamento de DST, AIDS e Hepatites Virais. http://sistemas.aids.gov.br. Acessado em 12/08/2013. Adaptado.)

Com base nos dados do gráfico, pode-se afirmar, corretamente, que,

Deseja-se formar uma comissão composta por sete membros do Senado Federal brasileiro, atendendo às seguintes condições: (i) nenhuma unidade da Federação terá dois membros na comissão, (ii) cada uma das duas regiões administrativas mais populosas terá dois membros e (iii) cada uma das outras três regiões terá um membro.

Segundo a Constituição da República Federativa do Brasil - 1988, cada unidade da Federação é representada por três senadores.

1. a) Quantas unidades da Federação tem cada região?
   

2. b) Chame de $N$ o número de comissões diferentes que podem ser formadas (duas comissões são consideradas iguais quando têm os mesmos membros). Encontre uma expressão para $N$ e simplifique-a de modo a obter sua decomposição em fatores primos.
   

3. c) Chame de $P$ a probabilidade de se obter uma comissão que satisfaça as condições exigidas, ao se escolher sete senadores ao acaso. Verifique que $P <\dfrac{1}{50}$.
   

A fenilcetonúria é uma doença que tem herança autossômica recessiva. Considere a prole de um casal de heterozigóticos quanto à mutação que causa a doença.

1. a) Qual é a probabilidade de o genótipo da primeira criança ser igual ao de seus genitores?
   

2. b) Qual é a probabilidade de as duas primeiras crianças apresentarem fenilcetonúria?
   

3. c) Se as duas primeiras crianças forem meninos que têm a doença, qual é a probabilidade de uma terceira criança ser uma menina saudável?
   

4. d) Se a primeira criança for clinicamente normal, qual é a probabilidade de ela não possuir a mutação que causa a fenilcetonúria?