UEL 2018 Matemática - Questões

Um estudante fez uma pesquisa com um grupo de universitários para obter um panorama a respeito da utilização de três redes sociais. Ao computar as informações fornecidas pelas pessoas entrevistadas, constatou que:

• 055 utilizam Snapchat, Instagram e Facebook;

• 070 utilizam Snapchat e Facebook;

• 105 utilizam Snapchat e Instagram;

• 160 utilizam Instagram e Facebook;

• 180 utilizam Snapchat;

• 225 utilizam Instagram;

• 340 utilizam Facebook;

• 085 não utilizam qualquer uma das redes sociais da pesquisa.

A partir dessas informações, quantas pessoas foram entrevistadas?

Justifique sua resposta, apresentando os cálculos realizados na resolução desta questão.

Considere a fórmula do termo geral de uma sequência finita de números primos, apresentada a seguir, em que $a_n$ representa o $n$-ésimo termo e $n$ corresponde a um número natural, tal que $1\le n\le 40$.

$$a_n=n^2-n+41$$

A partir dessas informações, responda aos itens a seguir.

1. a) Determine o primeiro e o último número primo dessa sequência. Justifique sua resposta, apresentando os cálculos realizados na resolução deste item.
   

2. b) Qual a posição do número primo 251 nessa sequência? Justifique sua resposta, apresentando os cálculos realizados na resolução deste item.
   

(Rivane Neuenschwander, Mal-entendido, casca de ovo, areia, água, vidro e fita mágica, 2000.)

Leia o texto e observe a figura a seguir.

O corpo da galinha sabe muito de geometria. Foi o ovo que me contou. Porque o ovo é um objeto geométrico construído segundo rigorosas relações matemáticas. A galinha nada sabe sobre geometria, na cabeça. Mas o corpo dela sabe. Prova disso é que ela bota esses assombros geométricos. Sabe muito também sobre anatomia. O ovo não é uma esfera.

(ALVES, R. O ovo. Correio Popular, Caderno C, 3 fev. 2002.)

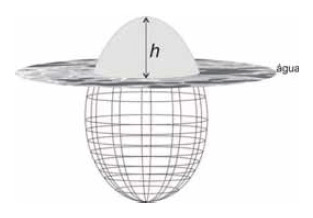
Dois valores positivos são necessários para descrever a geometria de um ovo: $R$ e $L$. Em função destes, o volume total $V$ do ovo é dado pela expressão $V=\pi R^2L$. Suponha que um ovo flutue em um copo d’água, conforme indicado na figura. Um matemático determina que o volume $S$ da parte submersa do ovo, em função da altura $h>0$ da parte que se encontra acima d’água, é dado pela equação a seguir.

$$S=\dfrac{\pi R^2}{L}\left(L^2-\dfrac{1}{2}h^2\right)$$

Considerando as equações, assinale a alternativa que apresenta, corretamente, o valor de $h$, sabendo que o volume da parte submersa corresponde a 80% do volume total do ovo.

Considere a equação polinomial a seguir.

$$2x^3-15x^2+34x-24=0$$

Sabe-se que cada uma das raízes dessa equação corresponde a uma das medidas, em cm, do comprimento, da largura e da altura de um paralelepípedo retângulo.

Com base nessa informação, determine a área total e o volume desse paralelepípedo.

Justifique sua resposta, apresentando os cálculos realizados na resolução desta questão.

Em uma população totalmente suscetível a uma doença infecciosa, o número de novas infecções $C(n)$, no instante de tempo $n$, cresce em progressão geométrica de razão $q>0$. Isto é, $C(n)=C_0q^n$, onde $n$ é expresso em uma certa unidade de medida e $C_0$ é a quantidade de infectados no instante inicial $n=0$.

A seguir, é apresentada uma tabela com exemplos.

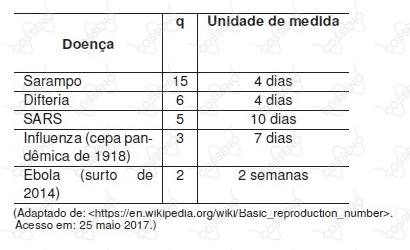
(Adaptado de: <https://en.wikipedia.org/wiki/Basic_reproduction_number>. Acesso em: 25 maio 2017.)

Suponha que uma cidade totalmente suscetível, na Europa medieval, tenha sido tomada pela Peste Negra, que se iniciou com $C_0 = 15$ infectados.

Considerando que, em 8 dias, a soma de infectados desde o início da infestação totalizou 195 pessoas e que a unidade de medida seja de 4 dias, assinale a alternativa que apresenta, corretamente, a razão $q$.