UEL 2012 - Questões

Considere que um tsunami se propaga como uma onda circular (Fig. 22).

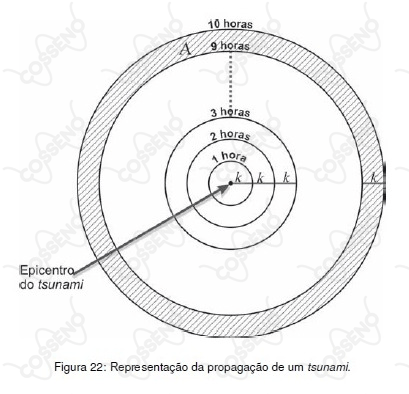
Figura 22: Representação da propagação de um tsunami.

Se a distância radial percorrida pelo tsunami, a cada intervalo de 1 hora, é de k quilômetros, então a área A, em quilômetros quadrados, varrida pela onda entre 9 horas e 10 horas é dada por:

A tabela a seguir apresenta a capacidade de geração de energia C, a área inundada A e a razão da capacidade de geração de energia pela área inundada $E=\dfrac{C}{A}$, de 5 usinas hidrelétricas brasileiras.

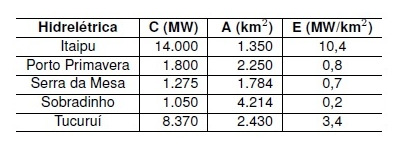
O maior valor de $E$ é aquele da usina de Itaipu. O par ordenado $(x; y)$ do sistema linear

$$\left[\begin{array}{cc} 3,4 & 0,2 \\ 0,8 & 0,7\end{array} \right] \left[ \begin{array}{cc}x\\y\end{array}\right] \left[ \begin{array}{c} 10,4 \\ 10,4\end{array}\right]$$

fornece a quantidade de vezes que se deve aumentar o valor de $E$ nos pares de usinas Tucuruí/Sobradinho e Porto Primavera/Serra da Mesa para que cada par ordenado tenha o mesmo valor E de Itaipu. Com base no enunciado e nos conhecimentos sobre matrizes, determinantes e sistemas lineares, considere as afirmativas a seguir.

1. I) O sistema linear dado tem infinitas soluções.
   

2. II) Para que a usina de Sobradinho tenha o mesmo E da usina de Tucuruí, é necessário que ela aumente $9,7$ vezes sua capacidade de geração de energia.
   

3. III) A matriz do sistema linear dado tem determinante não nulo, portanto a solução do sistema linear é única.
   

4. IV) Para que a usina de Porto Primavera tenha o mesmo E da usina de Itaipu, é necessário que ela aumente $13,0$ vezes sua capacidade de geração de energia.
   

Assinale a alternativa correta.

O gráfico de uma função f, figura 18, mostra o deslocamento vertical de um surfista sobre uma onda, em função do tempo.

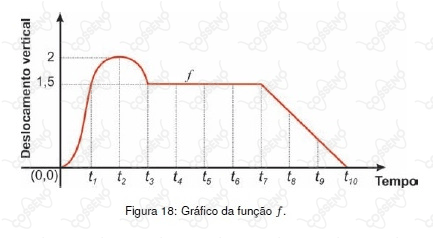
Figura 18: Gráfico da função f.

Com base no gráfico e nos conhecimentos sobre funções, considere as afirmativas a seguir.

1. I) Para todo $t\in (t_3; t_7$); $f$ é constante.
   

2. II) Para todo $t\in [0; t_3)$; $f(t) = \cos\ (t) + 2$.
   

3. III) Para todo $t\in (t_7; t_{10})$; $f(t) = m\cdot t + b$, onde $m > 0$.
   

4. IV) A função $f$ assume seu valor máximo em $t = t_2$.
   

Assinale a alternativa correta.

A escala Richter atribui um número $M$ para quantificar a magnitude de um tremor, ou seja, $M(A) = \log_{10}\ A - \log_{10}\ A_0$, onde $A > 0$ é a amplitude máxima das ondas sísmicas medidas a $100\ \text{km}$ do epicentro do sismo e $A_0 > 0$ é uma amplitude de referência. Por exemplo, em 1945, no Japão, o tremor gerado pela bomba atômica teve magnitude aproximada de 4,9 na escala Richter, enquanto que o tremor ocorrido naquele país, em março de 2011, teve magnitude de $8,9$.

Com base nessas informações, considere as afirmativas a seguir.

1. I) A amplitude máxima das ondas sísmicas do tremor de 2011 foi 10.000 vezes maior do que a amplitude máxima das ondas sísmicas geradas pela bomba de Hiroshima.
   

2. II) A diferença de magnitude de dois tremores, em relação às respectivas amplitudes máximas das ondas sísmicas, é uma função quadrática.
   

3. III) Um tremor de magnitude 8,0 na escala Richter tem ondas sísmicas com amplitude máxima 10 vezes maior do que a amplitude máxima em um tremor de magnitude 7,0.
   

4. IV) Se a amplitude máxima das ondas sísmicas de um tremor for menor que a amplitude de referência $A_0$, tem-se que a magnitude deste tremor é positiva.
   

Assinale a alternativa correta.

A figura a seguir representa um modelo plano do desenvolvimento vertical da raiz de uma planta do mangue. A partir do caule, surgem duas ramificações da raiz e em cada uma delas surgem mais duas ramificações e, assim, sucessivamente. O comprimento vertical de uma ramificação, dado pela distância vertical reta do início ao fim da mesma, é sempre a metade do comprimento da ramificação anterior.

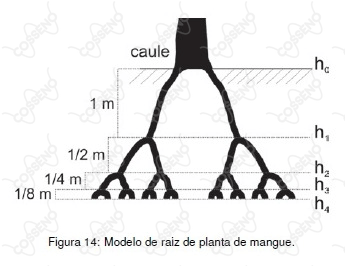Figura 14: Modelo de raiz de planta de mangue.

Sabendo que o comprimento vertical da primeira ramificação é de $h_1 = 1\ \text{m}$, qual o comprimento vertical total da raiz, em metros, até $h_{10}$?