IME 2011 Física - Questões
Abrir Opções Avançadas
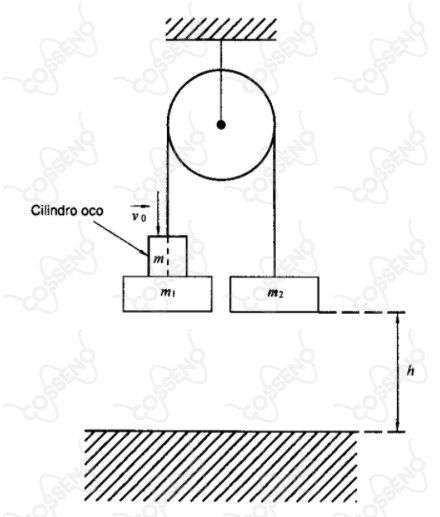
A figura acima apresenta duas massas $m_1= 5\ kg$ e $m_2 = 20\ kg$ presas por um fio que passa por uma roldana. As massas são abandonadas a partir do repouso, ambas a uma altura $h$ do solo, no exato instante em que um cilindro oco de massa $m = 5\ kg$ atinge $m_1$ com velocidade $v = 36\ m/s$, ficando ambas coladas. Determine a altura $h$, em metros, para que $m_1$ chegue ao solo com velocidade nula.
• Aceleração da gravidade: $g = 10\ m/s^2$
Observação:
• A roldana e o fio são ideais.
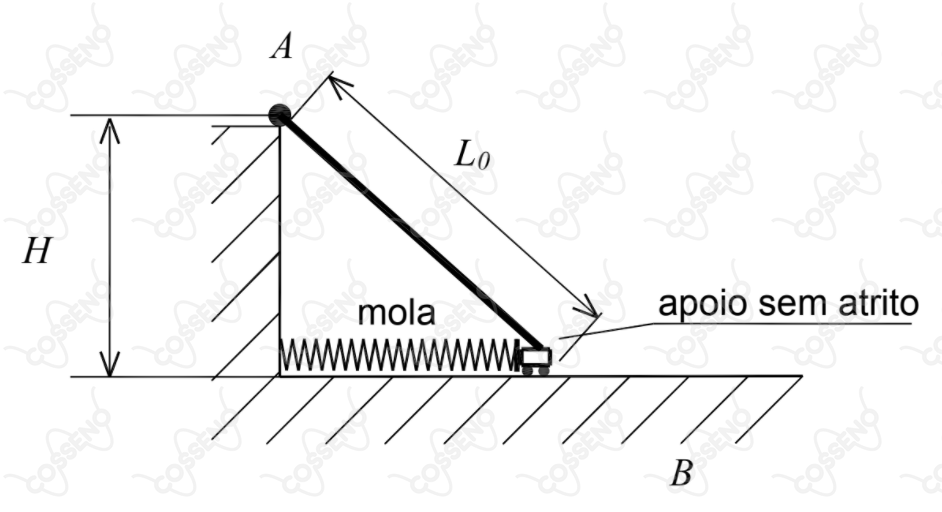
A figura acima mostra um sistema composto por uma parede vertical com altura $H$, uma barra com comprimento inicial $L_0$ e uma mola. A barra está apoiada em uma superfície horizontal sem atrito e presa no ponto $A$ por um vínculo, de forma que esta possa girar no plano da figura. A mola, inicialmente sem deformação, está conectada à parede vertical e à barra. Após ser aquecida, a barra atinge um novo estado de equilíbrio térmico e mecânico. Nessa situação a força de reação vertical no apoio $B$ tem módulo igual a $30\ N$. Determine a quantidade de calor recebida pela barra.
• $H = 3\ m$;
• $L_0 = 3\sqrt2\ m$;
• o peso da barra: $P = 30\ N$;
• constante elástica da mola: $k = 20\ N/m$;
• $\frac{Pc}{g\alpha}=\frac{50+30\sqrt2}{3\sqrt2}$ joules$,$ onde $c$ é o calor específico da barra; $\alpha$ é o coeficiente de dilatação linear da barra; $g$ é a aceleração da gravidade; e $P$ é o peso da barra.
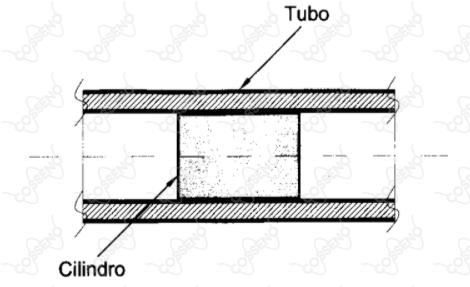
A figura acima apresenta um cilindro que executa um movimento simultâneo de translação e rotação com velocidades constantes no interior de um tubo longo. O cilindro está sempre coaxial ao tubo. A folga e o atrito entre o tubo e o cilindro são desprezíveis. Ao se deslocar no interior do tubo, o cilindro executa uma rotação completa em tomo do seu eixo a cada $600\ mm$ de comprimento do tubo. Sabendo que a velocidade de translação do cilindro é $6\ m/s$, a velocidade de rotação do cilindro em $rpm$ é:

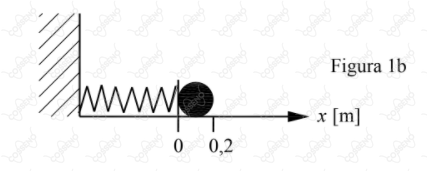

Um corpo está sobre um plano horizontal e ligado a uma mola. Ele começa a ser observado quando a mola tem máxima compressão (Figura 1a). Durante a observação, verificou-se que, para a deformação nula da mola (em $x = 0$), sua velocidade é $5\ m/s$ (Figura 1b). Para $x = 0,2\ m$ (Figura 1c), o corpo é liberado da mola a partir dessa posição e fica submetido a uma força de atrito até parar. Faça um gráfico da aceleração a do corpo em função da posição $x$, registrando os valores de $a$ e de $x$ quando:
a) a observação se inicia;
b) a velocidade é máxima;
c) o corpo é liberado da mola;
d) o corpo para.
• massa do corpo: $500\ g$;
• constante elástica da mola: $50\ N/m$;
• coeficiente de atrito entre o plano e o corpo: $0,3$.
Um observador e uma fonte sonora de frequência constante movem-se, respectivamente, segundo as equações temporais projetadas nos eixos $X$ e $Y$:
Observador | $X_0 (t) = \cos(t)$ | $Y_0(t) = -\cos(t)$ |
Fonte | $X_f(t) = \sin(t) + \cos(t)$ | $Y_f(t) = -2 \cos(t)$ |
Com relação ao instante $t (0 \leq t < \pi)$, o observador perceberá uma frequência:
• A velocidade de propagação da onda é muito maior que as velocidades do observador e da fonte.
Carregando...