IME 2001 Matemática - Questões
Abrir Opções Avançadas
Considere a figura abaixo, onde $\overline{AB} = \overline{AD} = 1{,} \ \overline{BC} = x{,} \ \overline{AC} = y{,} \ \overline{DE} = z$ e $\overline{AE} = w$. Os ângulos $D\hat{E}A$, $B\hat{C}A$ e $B\hat{F}A$ são retos.
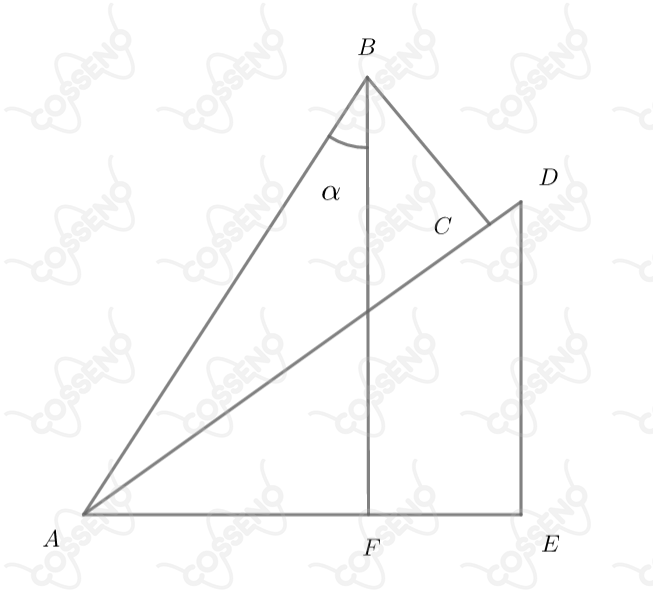
a) Determine o comprimento de $\overline{AF}$ e de $\overline{BF}$ em função de $x$, $y$, $z$ e $w$.
b) Determine a tangente do ângulo $\alpha$ em função de $x$, $y$, $z$ e $w$.
Considere o polinômio de grau mínimo, cuja representação gráfica passa pelos pontos $P_{1}(-2{,} \ -11){,} \ P_{2}(-1{,} \ 0){,} \ P_{3}(1{,} \ 4)$ e $P_{4}(2{,} \ 9)$.
a) Determine os coeficientes do polinômio.
b) Calcule todas as raízes do polinômio.
Determine todos os números inteiros $m$ e $n$ para os quais o polinômio $2x^m + a^{3n}x^{m - 3n} - a^m$ é divisível por $x + a$.
Sejam $a$ e $b$ números reais positivos e diferentes de $1$. Dado o sistema abaixo:
$\begin{cases} a^x \cdot b^{1/y} = \sqrt{ab} \\ 2 \cdot \log_{a}{x} = \log_{1/b}{y} \cdot \log_{\sqrt{a}}{b} \end{cases}$
determine os valores de $x$ e $y$.
Dois números complexos são ortogonais se suas representações gráficas forem perpendiculares entre si. Prove que dois números complexos $Z_1$ e $Z_2$ são ortogonais se e somente se:
$Z_{1} \overline{Z_{2}} + \overline{Z_{1}} Z_{2} = 0$
Obs: $\overline{Z}$ indica o conjugado de um número complexo $Z$.
Carregando...