EPCAR 2020 - Questões

Dona Lourdes trabalha em uma livraria, precisa guardar $200$ livros em $x$ caixas e vai utilizar todas elas.

Se em $30$ das $x$ caixas ela guardar $4$ livros em cada caixa e, nas demais, guardar $5$ livros em cada caixa, então, sobrarão alguns livros para serem guardados.

Entretanto, se em $20$ das $x$ caixas ela guardar $4$ livros em cada caixa e $5$ livros em cada uma das demais, então, não haverá livros suficientes para ocupar todas as caixas.

Assim, a soma dos algarismos do número $x$ é igual a

Para homenagear os aniversariantes do mês de junho, um grupo de alunos das turmas FOX e GOLF do esquadrão SABRE decidem fazer um churrasco comemorativo e dividir a despesa total.

Na véspera do churrasco, $6$ desses alunos foram convocados pelo seu Comandante para uma atividade que os impediu de comparecerem ao evento comemorativo, sendo esses $6$ alunos excluídos do rateio da despesa total.

Com a ausência desses $6$ alunos, foi cobrado de cada um dos demais, certo valor a mais.

Ao fazerem o rateio, os alunos perceberam que a despesa total era igual ao valor cobrado a mais de cada um dos alunos que contribuíram, multiplicado por $180$.

Se o número de alunos que foram ao churrasco é $K$, então, a soma dos algarismos de $K$ é

Uma pessoa aplicou $60.000$ reais durante o ano de $2018$. Parte desse dinheiro aplicou no investimento $P$ e a outra parte, no investimento $Q$.

No final de $2018$, retirou o dinheiro das duas aplicações e verificou que, somando os dois valores, não obteve lucro nem prejuízo. O investimento $P$ rendeu $10$%, mas, sobre o rendimento, foi cobrada uma taxa de $10$%; já o investimento $Q$ deu prejuízo de $12,6$%

Com base nessas informações, pode-se afirmar que

Um professor, após ter ministrado os conteúdos de função polinomial do 1º grau e função polinomial do 2º grau, elaborou, juntamente com os alunos do 9º ano, um projeto de uma pista virtual de um percurso de aviões em um jogo eletrônico.

A figura abaixo é a vista frontal dessa pista, num plano cartesiano, que é composta por:

• três percursos em linha reta: $\overline{AB}$, $\overline{OG}$, $\overline{LM}$; e

• duas curvas parabólicas: do ponto $B$ até o ponto $O$, com vértice em $C$, e do ponto $G$ ao ponto $L$, com vértice em $N$

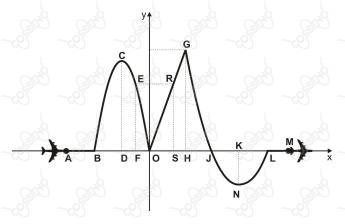
Sabe-se que:

$\overline{DO} = 2$ e $F$ é o ponto médio de $\overline{DO}$

$$\overline{EF} = 4\ \ \ \overline{OH} = 2\ \ \ \overline{GH} = 6$$

$$\overline{JL} = 2 \ \ \ \overline{AO} = \overline{OL} = 5 \ \ \ \overline{LM} = 2$$

$\overline{CD}$ e $\overline{KN}$ são eixos de simetria das curvas parabólicas.

Se todas as medidas indicadas têm a mesma unidade de comprimento, então, o valor de ( $\overline{CD} + \overline{DC} + \overline{OS} + \overline{OJ} )$ , nessa mesma unidade de comprimento, é

Considere as expressões $P$ e $Q$, com os números $a$, $b$ e $c$ reais positivos e distintos entre si.

$$P = \dfrac{(a^6 + b^6 + c^6)^2 - (a^6 - b^6 -c^6)^2}{b^6 + c^6}$$

$$Q = \dfrac{(b^{-1} - a^{-1})^{-1} - (b^{-1} + a^{-1})^{-1}}{(a^{-1} + b^{-1})^{-1}-(a^{-1}-b^{-1})^{-1}}$$

A expressão $\sqrt{Q\sqrt{P}}$ é representada por