CN 2016 - Questões

Filtro de Questões

Disciplina

Assuntos

Selecione uma disciplina antes de escolher o assunto

Abrir Opções Avançadas

Filtrar por resolução:

Todas

01 CN 2016 - Matemática

ABC é um triângulo equilátero. Seja D um ponto do plano de ABC, externo a esse triângulo, tal que DB intersecta AC em E, com E pertencendo ao lado AC. Sabe-se que $B\hat{A}D=A\hat{C}D=90^\circ$. Sendo assim, a razão entre as áreas dos triângulos BEC e ABE é

$\dfrac{1}{3}$

$\dfrac{1}{4}$

$\dfrac{2}{3}$

$\dfrac{1}{5}$

$\dfrac{2}{5}$

02 CN 2016 - Matemática

Observe a figura a seguir.

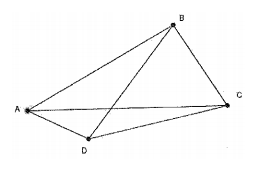
Seja ABC um triângulo retângulo de hipotenusa 6 e com catetos diferentes. Com relação à área ’S’ de ABC, pode-se afirmar que

será máxima quando um dos catetos for $3\sqrt{2}$

será máxima quando um dos ângulos internos for $30^\circ$

será máxima quando um cateto for dobro do outro.

será máxima quando a soma dos catetos dor $\dfrac{5\sqrt{2}}{2}$.

seu valor máximo não existe.

03 CN 2016 - Matemática

Seja $K=\left(\dfrac{999...997^2-9}{9999...994} \right)^3$ onde cada um dos números $9999...997$ e $9999...994$, são constituídos de 2015 algarismos 9. Deseja-se que $\sqrt{k}$ seja um número racional. Qual a maior potência de 2 que o índice i pode assumir?

$32$

$16$

$8$

$4$

$2$

04 CN 2016 - Matemática

O número de divisores de $10^{2015}$ que são múltiplos de $10^{2019}$ é

$152$

$196$

$216$

$256$

$276$

05 CN 2016 - Matemática

No triângulo isósceles $ABC$, $AB=AC=13$ e $BC=10$. Em $AC$ marca-se $R$ e $S$, com $CR=2x$ e $CS=x$. Paralelo a $AB$ e passando por $S$ traça-se o segmento $ST$, com $T$ em $BC$. Por fim, marcam-se $U$, $P$ e Q simétricos de $T$, $S$ e $R$, nessa ordem, e relativo à altura de $ABC$ com pé sobre $BC$. Ao analisar a medida inteira $x$ para que a área do hexágono PQRSTU seja máxima, obtém-se:

$5$

$4$

$3$

$2$

$1$

Carregando...