AFA 2018 Física - Questões
Abrir Opções Avançadas
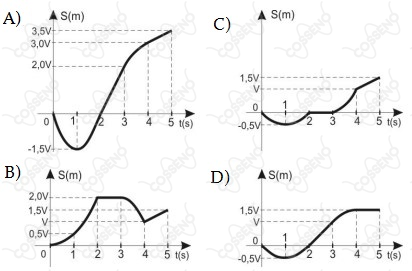
O gráfico seguinte representa a velocidade escalar $v$ de uma partícula em movimento retilíneo.

Considerando que, em $t = 0$, a partícula está na origem dos espaços $(S_0=0)$, o gráfico que melhor representa a posição $(S)$ dessa partícula até o instante $t = \pu{5 s}$ é
Uma partícula é abandonada sobre um plano inclinado, a partir do repouso no ponto $A$, de altura $h$, como indicado pela figura (fora de escala). Após descer o plano inclinado, a partícula se move horizontalmente até atingir o ponto $B$. As forças de resistência ao movimento de $A$ até $B$ são desprezíveis. A partir do ponto $B$, a partícula então cai, livre da ação de resistência do ar, em um poço de profundidade igual a $3h$ e diâmetro $x$. Ela colide com o chão do fundo do poço e sobe, em uma nova trajetória parabólica até atingir o ponto $C$, o mais alto dessa nova trajetória. Na colisão com o fundo do poço a partícula perde $50\%$ de sua energia mecânica. Finalmente, do ponto $C$ ao ponto $D$, a partícula move-se horizontalmente experimentando atrito com a superfície. Após percorrer a distância entre $C$ e $D$, igual a $3h$, a partícula atinge o repouso.

Considerando que os pontos $B$ e $C$ estão na borda do poço, que o coeficiente de atrito dinâmico entre a partícula e o trecho $\overline{CD}$ é igual a $0{,}5$ e que durante a colisão com o fundo do poço a partícula não desliza, a razão entre o diâmetro do poço e a altura de onde foi abandonada a partícula, $\dfrac{x}{h}$, vale
Para avaliar o papel da “Downforce”, considere um carro de Fórmula 1, de massa $M$, realizando uma curva em determinada pista plana. Ao se desprezar completamente os efeitos produzidos pelo seu movimento em relação ao ar, mas considerando o atrito entre pneus e o asfalto, o carro consegue fazer a curva, sem derrapar, a uma velocidade máxima $V$. Porém, ao levar em conta, especificamente, a atuação da “Downforce” $D$ (desconsiderando a força de arrasto) a velocidade máxima $V'$ do carro, nessa mesma curva, muda em função de $D$. Nessas condições, o gráfico que melhor representa a relação $\dfrac{V'}{V}$ em função de $D$ é

Um corpo $M$ de dimensões desprezíveis e massa $\pu{10 kg}$ movimentando-se em uma dimensão, inicialmente com velocidade $\vec{V}$, vai sucessivamente colidindo inelasticamente com $N$ partículas $m$, todas de mesma massa $\pu{1 kg}$, e com velocidades de módulo $v = \pu{20 m/s}$, que também se movimentam em uma dimensão de acordo com a Figura 1, a seguir.

O gráfico que representa a velocidade final do conjunto $v_f$ após cada colisão em função do número de partículas $N$ é apresentado na Figura 2, a seguir.
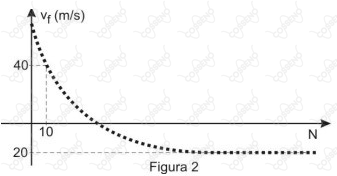
Desconsiderando as forças de atrito e a resistência do ar sobre o corpo e as partículas, a colisão de ordem $N_o$ na qual a velocidade do corpo resultante (corpo $M + N_o$ partículas $m$) se anula, é,
Uma rampa, homogênea, de massa $m$ e comprimento $L$, é inicialmente colocada na horizontal. A extremidade $A$, dessa rampa, encontra-se acoplada a uma articulação sem atrito. Na extremidade $B$ está sentado, em repouso, um garoto, também de massa $m$. Essa extremidade $B$ está presa ao chão, por um fio ideal, e ao teto, por uma mola ideal, de constante elástica $k$, conforme ilustra a Figura 1.
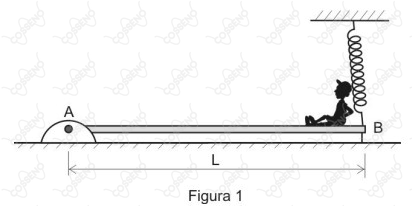
Em um determinado instante o garoto corta o fio. A mola, que está inicialmente deformada de um valor $\Delta{x}$ , passa a erguer lentamente a extremidade $B$ da rampa, fazendo com que o garoto escorregue, sem atrito e sem perder o contato com a rampa, até a extremidade $A$, conforme Figura 2.

Quando o garoto, que neste caso deve ser tratado como partícula, atinge a extremidade $A$, a mola se encontra em seu comprimento natural (sem deformação) e a rampa estará em repouso e inclinada de um ângulo $\theta$. Considerando $g$ o módulo da aceleração da gravidade local, nessas condições, a velocidade do garoto em $A$, vale
Carregando...