AFA 2015 - Questões

Filtro de Questões

Abrir Opções Avançadas

Filtrar por resolução:

01 AFA 2015 - Matemática

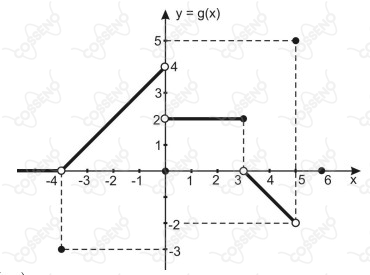
Considere o gráfico da função real $g: A \to A$ abaixo e marque (V) verdadeiro ou (F) falso.

($\space \space \space$) A função $g$ possui exatamente duas raízes.

($\space \space \space$) $g(4) = -g(-3)$

($\space \space \space$) $Im(g) = \{-3 \} \space \cup \space ]-2, 4[$

($\space \space \space$) A função definida por $h(x) = g(x) + 3$ NÃO possui raiz.

($\space \space \space$) $(g \circ g \circ g \circ \cdots \circ g) (-2) = 2$

A sequência correta é

F - V - F - F - V

F - F - V - F - V

F - V - F - V - F

V - V - F - F - V

02 AFA 2015 - Matemática

No Atlas de Desenvolvimento Humano no Brasil $2013$ constam valores do Índice de Desenvolvimento Humano Municipal (IDHM) de todas as cidades dos estados brasileiros.

O IDHM é um número que varia entre $0$ e $1$. Quanto mais próximo de $1$, maior o desenvolvimento humano de um município, conforme escala a seguir.

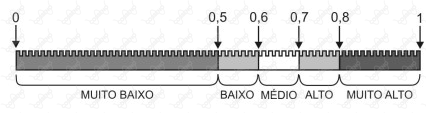
Abaixo estão relacionados o IDHM de duas cidades de Minas Gerais em condições extremas, Monte Formoso e Uberlândia, e uma em situação intermediária, Barbacena.

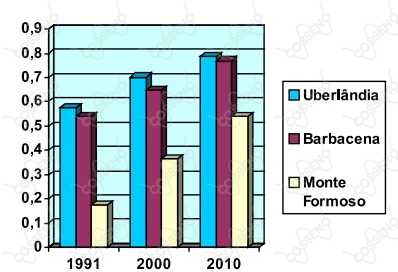
Analisando os dados acima, afirma-se que

I. o município de maior crescimento do IDHM, nos períodos considerados, é Monte Formoso.

II. na última década, Barbacena apresentou maior evolução do IDHM que Uberlândia.

III. uma tabela que relaciona cidade, época e faixa de IDHM pode ser representada corretamente como:

São corretas

apenas l e ll

apenas lI e III

apenas l e Ill

I, ll e lll

03 AFA 2015 - Matemática

Considere num mesmo sistema cartesiano ortogonal as funções reais $f$, $g$ e $h$ tais que:

$f$ é função quadrática cujo vértice $V$ é simétrico do ponto $P(0, -27)$, em relação ao eixo $\overrightarrow{\rm OX}$;
$g$ é função afim que passa pelos pontos $Q(-1,12)$ e $R(3,0)$;
os pontos $Q$ e $R$ também pertencem à função $f$;
$h$ é uma função constante cujo gráfico intercepta o gráfico da função $g$ no ponto de abscissa $-7$.

Analise os gráficos das funções $f$, $g$ e $h$ e marque a alternativa correta.

$g(x) \geq f(x)$ se, e somente se, $\{ x \in \mathbb{R} \space | \space x \geq 3 \}$

A função real $j$ dada por $j(x) = \sqrt{-f(x) \cdot g(x)}$ está definida se, e somente se, $x \in \space ] -\infty, 3]$

Se $-1 \leq x \leq 3$, então $f(x) \geq g(x) $

$f(x) < g(x) \leq h(x)$, $\forall \space x \in \mathbb{R}$ tal que $x \geq -7$

04 AFA 2015 - Matemática

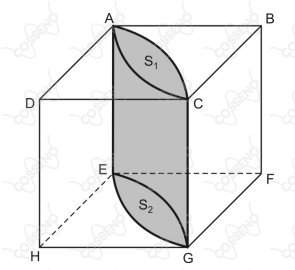
Na figura abaixo, tem-se um cubo cuja aresta mede $k$ centímetros; as superfícies $S_{1}$ e $S_{2}$, contidas nas faces desse cubo, são limitadas por arcos de circunferências de raio $k$ centímetros e centros em, respectivamente, $D$ e $B$, $H$ e $F$.

O volume do sólido formado por todos os segmentos de reta com extremidades em $S_{1}$ e $S_{2}$, paralelos a $\overline{\rm CG}$ e de bases $S_{1}$ e $S_{2}$, é, em $\pu{cm3}$, igual a

$\frac{k^{3} (\pi - 1)}{2}$

$\frac{k^{3} (\pi - 2)}{ 2}$

$\frac{k^{3} (\pi - 1)}{4}$

$\frac{k^{3} (\pi - 2)}{4}$

05 AFA 2015 - Matemática

Alex possui apenas moedas de $25$ centavos, de $50$ centavos e de $1$ real, totalizando $36$ moedas. Sabe-se que a soma do número de moedas de $25$ centavos com o dobro do número de moedas de $50$ centavos é igual à diferença entre $82$ e $5$ vezes o número de moedas de $1$ real. Nessas condições é correto afirmar que

esse problema possui no máximo $7$ soluções.

o número de moedas de $25$ centavos nunca será igual ao número de moedas de $50$ centavos.

o número de moedas de $50$ centavos poderá ser igual à soma do número de moedas de $25$ centavos com as de $1$ real.

o número de moedas de $1$ real pode ser $3$

Carregando...