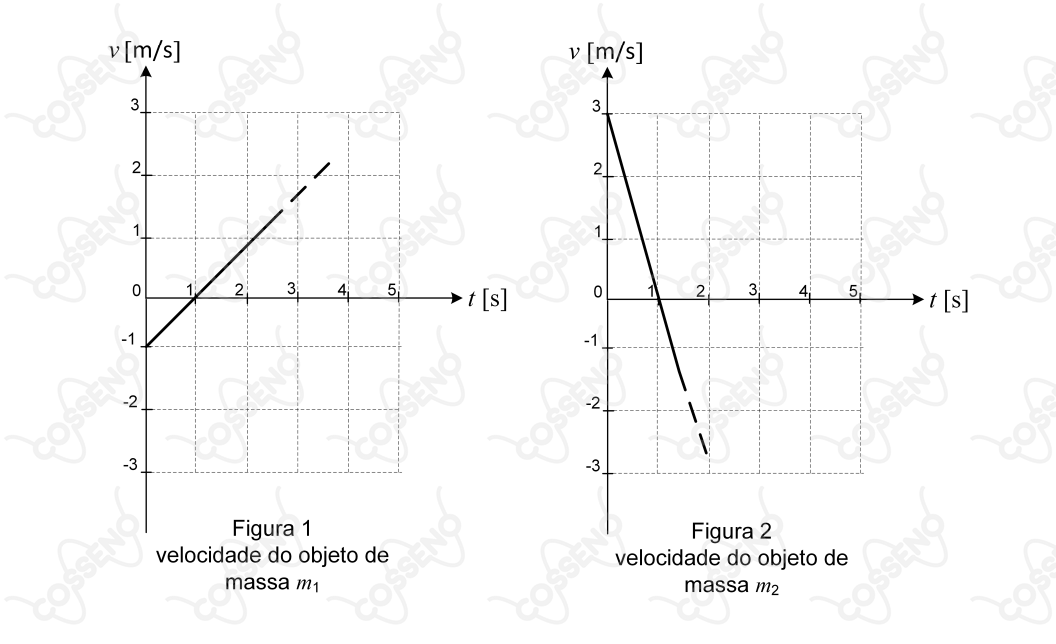
Em um experimento, dois objetos de massas e partem, respectivamente, das posições e do mesmo eixo horizontal. Suas velocidades são programadas de acordo com os gráficos lineares mostrados nas Figuras 1 e 2, até que, na iminência de colisão perfeitamente inelástica entre elas, o sistema de controle das velocidades é desativado, mantendo-se a inércia de seus movimentos.
A razão para que, após a colisão, os objetos retornem unidos à posição e com velocidade constante de módulo 2 é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Leis de formação dos gráficos $v\space$ x $\space t$ : $v_1 (t)= t-1$ e $v_2 (t)= -3t+3$ .
Dos instantes $0$ a $1$ segundos, as distâncias percorridas pelas partículas de massas $m_1$ e $m_2$ são, respectivamente, iguais a $0,5\space m$ e $1,5\space m$. Desse modo, ao final do intervalo de tempo, as velocidades instantâneas de cada partícula são nulas, ademais, a distância entre elas é de $32\space m$ .
Graficamente, interpreta-se que os módulos da aceleração de cada partícula são $a_1 = 1\space m/s^2$ e $a_2 = 3\space m/s^2$, desconsiderando a orientação do deslocamento. Seja $t_c$ o tempo levado até que as partículas se choquem frontalmente, e $t_{total} = t_c + 1$, o tempo total desde o instante $\space 0$, temos:$$\frac{1\cdot t_c^2}{2} + \frac{3\cdot t_c^2}{2} = 2\cdot t_c^2 = 32 \implies t_c = 4s \implies t_{total} = 5s$$Assim, podemos encontrar os valores absolutos velocidades, no instante da colisão:$$|v_1(5)| = 4\space m/s \space \space \space \text{e} \space \space \space |v_2(5)| = 12\space m/s$$Pela conservação da quantidade de movimento, e considerando as condições do enunciado, temos:$$4m_1 - 12m_2 =-2\cdot (m_1+m_2) \implies 6m_2 - 2m_1 = m_1 + m_2$$Portanto, obtêm-se: $\space 5m_2 = 3m_1$ $\implies$ $\boxed{\large{\frac{m_2}{m_1} = \frac{3}{5}}}$ $\text{Alternativa } \mathbb{(E)}$

