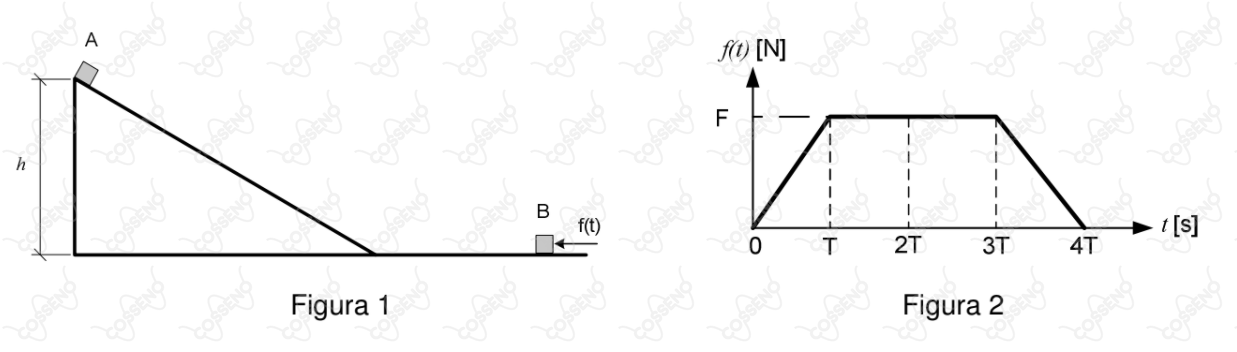
Na Figura 1, o corpo , constituído de gelo, possui massa e é solto em uma rampa a uma altura . Enquanto desliza pela rampa, ele derrete e alcança o plano horizontal com metade da energia mecânica e metade da massa iniciais. Após atingir o plano horizontal, o corpo se choca, no instante , com o corpo B, de massa , que foi retirado do repouso através da aplicação da força , cujo gráfico é exibido na Figura 2.
Para que os corpos parem no momento do choque, deve ser dado por
Dado:
• aceleração da gravidade: $g$.
Observações: • o choque entre os corpos é perfeitamente inelástico; • o corpo não perde massa ao longo de seu movimento no plano horizontal.
Observações: • o choque entre os corpos é perfeitamente inelástico; • o corpo não perde massa ao longo de seu movimento no plano horizontal.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Energia mecânica inicial do gelo: $E_{mec(i)} = mgh$
Energia mecânica final do gelo: $E_{mec(f)} = \frac{E_{mec(i)}}{2}$ $\implies$ $\large{\frac{mv_f^2}{4} = \frac{mgh}{2}}$ $\implies$ $\color{green}{v_f = \sqrt{2gh}}$
Em que $v_f$ é a velocidade do bloco de gelo, ao atingir o plano horizontal.
Em relação ao corpo B, o impulso da força $f(t)$ será numericamente igual a área sob gráfico, formado por esta função, como representado na figura 2. Como B é retirado do repouso, a sua quantidade de movimento será igual ao impulso total de $f(t)$.
Sendo $v_b$ a velocidade adquirida pelo bloco B, temos:$$m\cdot v_b = 3\cdot F\cdot T \implies \color{green}{v_b = \frac{3FT}{m}}$$Como a colisão é inelástica, para que os corpos parem, a velocidade escalar do conjunto deverá ser nula. Pela conservação da quantidade de movimento, temos:$$\frac{m}{2}\cdot \sqrt{2gh\space } - m\cdot \frac{3FT}{m} = 0 \implies \boxed{F = \frac{m\sqrt{2gh\space}}{6T}}$$
$$\text{Alternativa } \mathbb{(B)}$$

