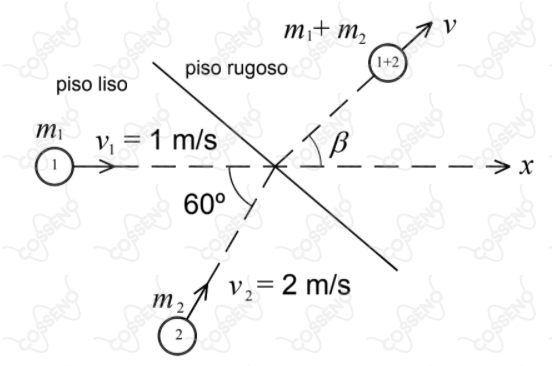
Duas bolas, e , movem-se em um piso perfeitamente liso. A bola , de massa , move-se no sentido da esquerda para direita com velocidade . A bola , de massa , move-se com ângulo de com o eixo , com velocidade . Sabe-se que o coeficiente de atrito cinético entre as bolas e o piso rugoso é e a aceleração gravitacional é . Ao colidirem, permanecem unidas após o choque e movimentam-se em um outro piso rugoso, conforme mostra a figura. A distância percorrida, em metros, pelo conjunto bola e bola até parar é igual a
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A quantidade de movimento se conserva na colisão, por se tratar de um sistema isolado. Assim, podemos escrever as seguintes equações de conservação da quantidade de movimento
$\textbf{Eixo horizontal:}$ $$m_1v_1 + m_2v_2\cos 60^{\circ} = (m_1+m_2)\cdot v\cos\beta$$
$\textbf{Eixo vertical:}$ $$m_2v_2\sin 60^{\circ} = (m_1+m_2)\cdot v\sin\beta$$
Assim, substituindo os valores de seno e cosseno de $60^{\circ}$, chegamos a: $$\begin{align}\cos\beta&=\dfrac{1}{v} \\ \sin\beta&=\dfrac{\sqrt{3}}{3v}\end{align}$$
E assim, podemos usar a equação fundamental da trigonometria para descobrir o valor de $v$: $$\sin^2\beta+\cos^2\beta=1 \\ \dfrac{3}{9v^2}+\dfrac{1}{v^2}=1\\ v= \sqrt{\dfrac{4}{3}}\text{ m/s}$$
Agora podemos calcular a aceleração do objeto ao entrar no piso rugoso. A força de atrito tem módulo $\mu\cdot (m_1+m_2)g$, sendo $\mu = 0{,}10\sec^2\beta$. Assim: $$\mu=0{,}10\cdot \left(\dfrac{1}{v}\right)^2 \\ \mu=0{,}10\cdot \dfrac{3}{4} \\ \mu = 0{,}075$$
E assim a aceleração resultante será $$\begin{align}a_r&=\dfrac{F_r}{m_1+m_2} \\ a_r &= \dfrac{\mu\cdot (m_1+m_2)g}{(m_1+m_2)}\\ a_r &= \mu g \\ a_r &= \pu{0,75 m/s2}\end{align}$$
E assim, com a equação de Torricelli, podemos determinar a distância que o objeto percorre até parar. Repare que adotamos o sinal negativo para a aceleração, pois o movimento é retardado. $$\begin{align}v^2 &= v^2_0 +
2a_r \Delta s \\ 0 &= v^2 + 2\cdot (-0{,}75)\cdot \Delta s \\ 1{,}5\cdot\Delta s &= \dfrac{4}{3}\end{align}\\ \boxed{\Delta s = \pu{0,5 m}}\Rightarrow\text{Gab. B)}$$

