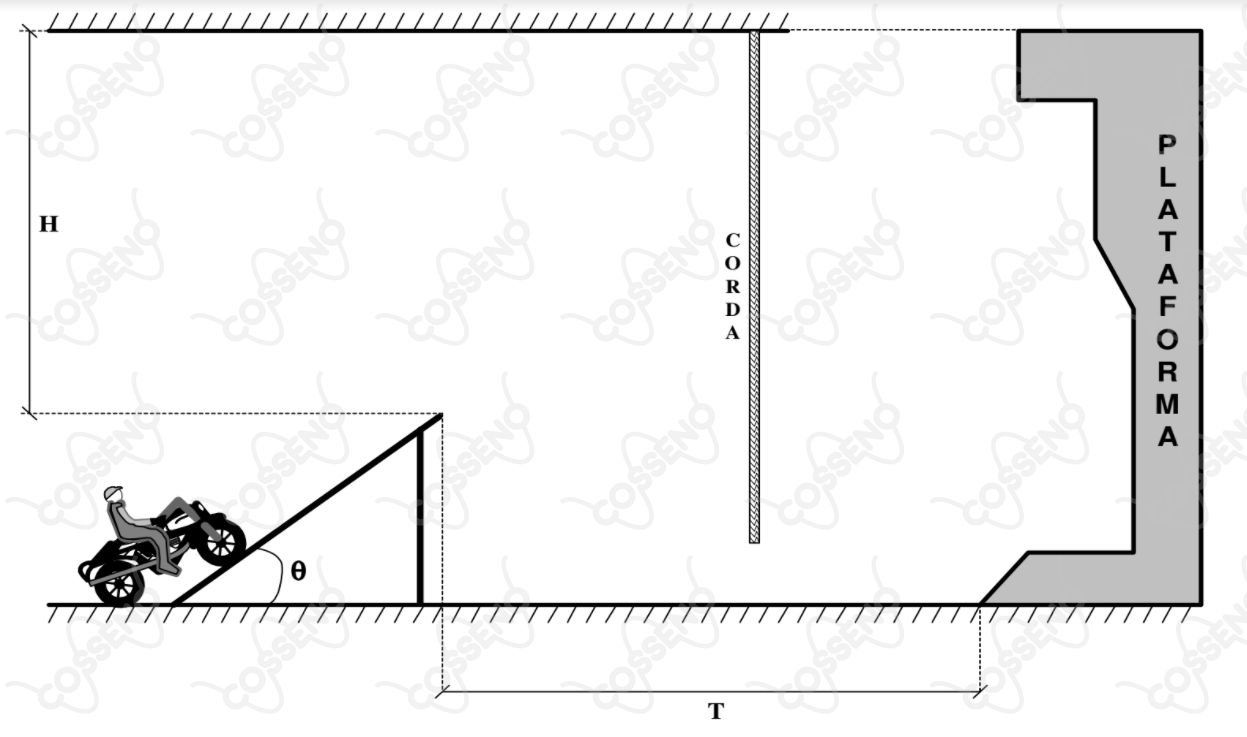
Um motociclista de massa deseja alcançar o topo de uma plataforma. Para isso, ele faz uso de uma moto de massa , uma corda inextensível de massa desprezível e uma rampa de inclinação . Ao saltar da rampa, o motociclista atinge a corda na situação em que esta permanece esticada e o esforço despendido por ele é o menor possível. Para evitar ruptura por excesso de peso, o motociclista libera a moto no momento do contato com a corda, que o conduz para o topo da plataforma.
Nestas condições, determine o vetor velocidade do motociclista na saída da rampa.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Primeiramente, observe que, para que a corda seja atingida esticada e o esforço do motorista seja mínimo, ele deve atingi-la com velocidade horizontal. Assim, o motorista atinge a corda no ápice da trajetória parabólica.
Seja $\ell$ o trecho de corda efetivo que o motorista usa para atingir o topo da plataforma. Então a altura máxima da trajetória parabólica é $H-\ell$ e em seguida ele realiza $1/4$ de uma circunferência de raio $\ell$. Observe também que o alcance percorrido pela parábola corresponde a metade do alcance total caso ele não se dependurasse na corda, tal metade vale $T - \ell$. Queremos calcular $\vec{v_0}$
Trajetória parabólica:
Na vertical, por Torricelli: $0 = (v_0 \cdot \sin{\theta})^2 - 2g(H-\ell) \Rightarrow v_0^2 = \frac{2g(H-\ell)}{\sin^2{\theta}}$
Na horizontal, o alcance total vale $A = \frac{v_0^2}{g}\sin{2\theta} = 2(T-\ell)$
Finalmente, retirando $\ell$ subtraindo-se as equações, podemos isolar $v_0$, obtendo $$v_0 = \sqrt{\frac{2g(T-H)}{\sin{2\theta} - \sin^2{\theta}}}$$ e $\vec{v_0}$ faz um ângulo de $\theta$ com a horizontal (convenção do ciclo trigonométrico)


