Umas das formas rápidas - numa situação de prova, por exemplo - de resolver esta questão é graficamente, pois assim se torna mais fácil analisar certas transformações termodinâmicas. No plano PV abaixo, consideremos os gráficos roxo e laranja como sendo, respectivamente, a isotérmica e a adiabática. 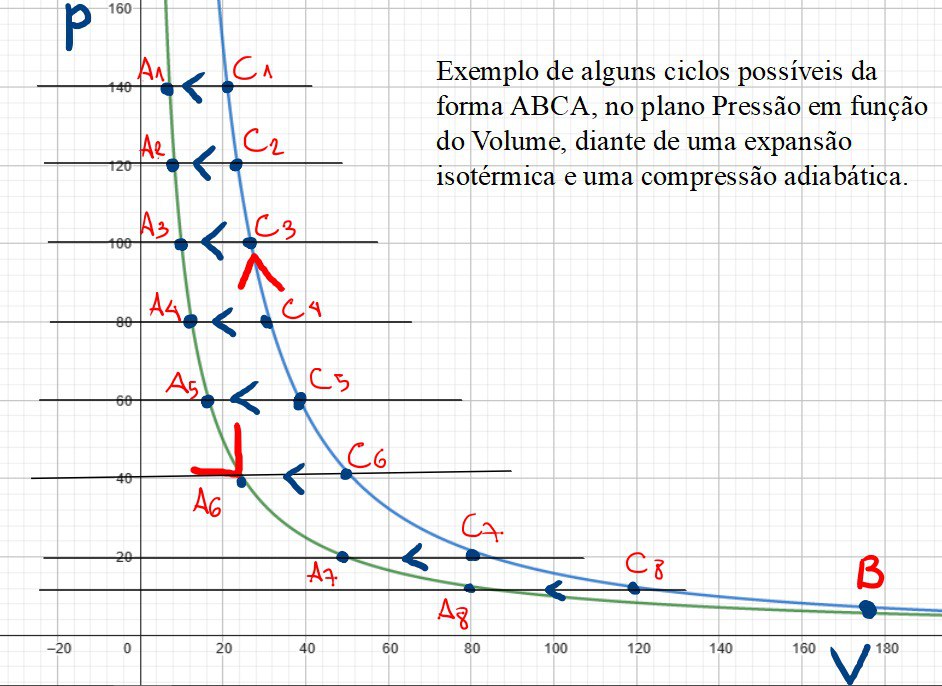No estudo da Termodinâmica, entende-se que a variação da energia interna poderá ser nula quando as transformações realizam um ciclo termodinâmico. No caso dos gráficos acima, a única alternativa que condiz com a realização de um ciclo é uma transformação isobárica, necessariamente uma compressão. Há vários argumentos gráficos para a primeira afirmativa. Um dos mais evidentes é o fato de que, na medida em que o volume decresce, as transformações isotérmica e adiabática tendem a permanecerem paralelas. Logo, para uní-las, uma das formas possíveis seria uma reta que corta esses dois gráficos, além de passar perpendicularmente pelo eixo P, o que por consequência torna uma transformação a pressão constante, isto é, uma isobárica. A segunda afirmativa - ser necessariamente uma compressão -, isto se dá simplesmente pela ordem em que o ciclo é realizado. Enfim, isso tudo é uma análise gráfica, e ao tentar achar resultados com as outras alternativas, haverão contradições - que não convém, por agora, citá-las -, encontrando apenas a alternativa ( C ) como resposta.