Na base de um plano inclinado com ângulo há uma carga puntiforme fixa. Sobre o plano inclinado a uma distância há uma massa de dimensões desprezíveis e carga . O coeficiente de atrito entre e o plano é . Um fio ideal preso em passa por uma roldana ideal e suspende um corpo de volume e densidade , totalmente imerso em um fluido de densidade . Considere a aceleração da gravidade como e a constante eletrostática do meio onde se encontra o plano como .
Determine, em função dos dados literais fornecidos, a expressão do valor mínimo da densidade do fluido para que permaneça imóvel sobre o plano inclinado.
CossenoGPT
Teste
gratuitamente agora
mesmo! 
$-$ Separando os corpos e colocando as forças atuantes nos mesmos, têm-se:
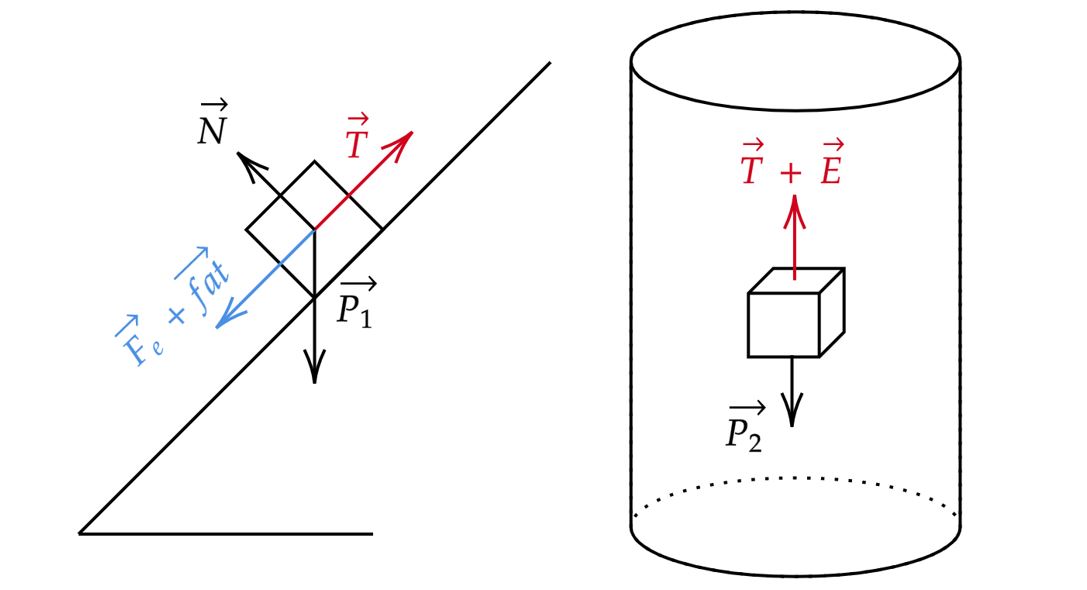Começando pelo bloco no plano inclinado, ao decompor a força peso encontramos:
\begin{matrix} T = fat +|F_e |+ P_1\sin{\alpha} &&,&& P_1\cos{\alpha} = N
\end{matrix} Assim, \begin{matrix} T &=& \mu . M_1 . g . \cos{\alpha} &+& \large{\frac{2KQ^2}{D^2}} &+& M_1.g.\sin{\alpha}
\end{matrix} Já no bloco imerso, temos:
\begin{matrix} T + E = P_2 \\ \\ ( \mu . M_1 . g . \cos{\alpha} + \frac{2KQ^2}{D^2} + M_1.g.\sin{\alpha}) + \rho_A .g.V_2 = M_2.g
\end{matrix} Como $M_2 = \rho_2 .V_2$ \begin{matrix} \rho_A &=& \rho_2 &-& \frac{1}{V_2}[ \ \frac{2KQ^2}{gD^2} &+& M_1 (\mu\cos{\theta} + \sin{\theta}) \ ]
\end{matrix}
$\color{orangered}{Adendo:}$ Perceba que, a tendência de movimento é o bloco da rampa subir, pense no bloco imerso, agora sem o fluido, se a tendência fosse o bloco descer a rampa, nunca teríamos equilíbrio ao adicionar o líquido, pois o empuxo contribuiria com o movimento!
Ampliar Imagem
