A situação-problema pode ser diagramada tal que: 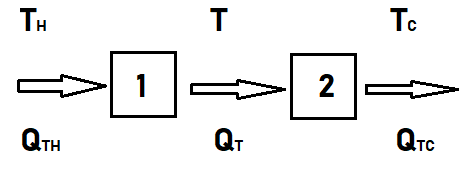Onde $T_H$ e $Q_{TH}$ são a temperatura e o calor de entrada da máquina térmica 1; $T$ e $Q_T$ são, a temperatura e o calor de saída da máquina térmica 1, e também de entrada da máquina térmica 2; e, por fim, $T_C$ e $Q_{TC}$ são a temperatura e o calor de saída da máquina térmica 2. Ambas máquinas operam em ciclo de Carnot. ITEM A: Rendimento dos dois ciclos é o mesmo. Para o ciclo de Carnot, o rendimento é tal que: $$\eta=1-\frac{T_F}{T_Q}$$ Logo, teremos para as máquinas 1 e 2: $$\eta_1=1-\frac{T}{T_H}\ ;\ \eta_2=1-\frac{T_C}{T}$$ Então, igualamos os dois rendimentos e chegamos à resposta: $$\eta_1=\eta_2 \Leftrightarrow 1-\frac{T}{T_H}=1-\frac{T_C}{T}$$ $$\boxed{T=\sqrt{T_HT_C}}$$ ITEM B: O trabalho em cada um dos ciclos é o mesmo. Para o ciclo de Carnot, o trabalho é tal que:$$W=Q_Q-Q_F$$Logo:$$W_1=Q_{TH}-Q_T\ ;\ W_2=Q_T-Q_{TC}$$ Então, igualamos os dois trabalhos e obtemos: $$W_1=W_1\Leftrightarrow Q_{TH}-Q_T=Q_T-Q_{TC}$$ $$2Q_T=Q_{TH}+Q_{TC}\Leftrightarrow Q_T=\frac{Q_{TH}+Q_{TC}}{2}\ (i)$$ Mas também sabemos que, para o ciclo de Carnot: $$\frac{Q_F}{Q_Q}=\frac{T_F}{T_Q} \Rightarrow \frac{Q_T}{Q_{TH}}=\frac{T}{T_H}\Rightarrow Q_T=\frac{T\cdot Q_{TH}}{T_H}\ (ii)$$ $$\frac{Q_{TC}}{Q_{TH}}=\frac{T_C}{T_H} \Rightarrow Q_{TC}=\frac{T_C\cdot Q_{TH}}{T_H}\ (iii)$$ Então igualamos (i) e (ii), substituímos (iii) na igualdade e chegamos à resposta: $$\frac{Q_{TH}+Q_{TC}}{2}=\frac{T\cdot Q_{TH}}{T_H} \Leftrightarrow \frac{Q_{TH}+Q_{TC}}{2Q_{TH}}=\frac{T}{T_H}$$ $$\frac{Q_{TH}}{2Q_{TH}}+\frac{\frac{T_C\cdot Q_{TH}}{T_H}}{2Q_{TH}}=\frac{T}{T_H} \Leftrightarrow \frac{1}{2}+\frac{T_C}{2T_H}=\frac{T}{T_H}$$ $$\boxed{T=\frac{T_H+T_C}{2}}$$

$\text{a)} $ o rendimento no primeiro caso é dado por $1 - \dfrac{T_{H}}{T}$ , e no segundo o rendimento é dado por $1 - \dfrac{T}{T_{C}}$ , como os rendimentos devem ser iguais , então : $1 - \dfrac{T_{H}}{T} =1 - \dfrac{T}{T_{C}} \implies \boxed{T = \sqrt{T_{H}T_{C}}} $ $\text{b)} $ Note que o trabalho desenvolvido pelos dois ciclos são igual , portanto : $Q_{H} - Q_{T} = Q_{T} - Q_{C} \implies Q_{T} = \dfrac{Q_{H} + Q_{C}}{2}$ Como $\dfrac{Q_{H}}{Q_{T}} = \dfrac{T_{H}}{T}$ e $\dfrac{Q_{C}}{Q_{T}} = \dfrac{T_{C}}{T}$ , portanto : $ 1 = \dfrac{\dfrac{Q_{H}}{Q_{T}} + \dfrac{Q_{C}}{Q_{T}} }{2} = \dfrac{\dfrac{T_{H}}{T} + \dfrac{T_{C}}{T} }{2} \implies \boxed{T = \dfrac{T_{H} + T_{C}}{2}} $