Dois números complexos são ortogonais se suas representações gráficas forem perpendiculares entre si. Prove que dois números complexos e são ortogonais se e somente se:
Obs: indica o conjugado de um número complexo .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$-$ A priori, sabemos que o argumento de um complexo é:
\begin{matrix} arg(z) &=& \tan^{-1}{z}
\end{matrix} $-$ Além disso, é sabido que: \begin{matrix}
arg{(z.w)} = arg(z) + arg(w) &,& arg(\overline{z}) = -arg(z)
\end{matrix}
$-$ Dessa forma, segundo enunciado, os dois complexos são ortogonais, o que significa:
\begin{matrix} (1):&& arg(z_1) - arg(z_2) &=& arg(z_1) + arg(\overline{z_2}) &=& arg{(z_1.\overline{z_2})}&=& \pm \frac{\pi}{2}
\\ \\
(2):&& arg(z_2) - arg(z_1) &=&arg(z_1) + arg(\overline{z_2}) &=& arg{(z_2.\overline{z_1})} &=& \mp\frac{\pi}{2}
\end{matrix} $-$ Fazendo $(1)+(2)$ , temos:
\begin{matrix} arg{(z_1.\overline{z_2})} &+& arg{(z_2.\overline{z_1})} &=& 0 \\ \\ (z_1.\overline{z_2}) &+& (z_2.\overline{z_1}) &=& 0
\end{matrix} $\color{orangered}{Obs:}$ Visualizando uma situação ortogonal qualquer:
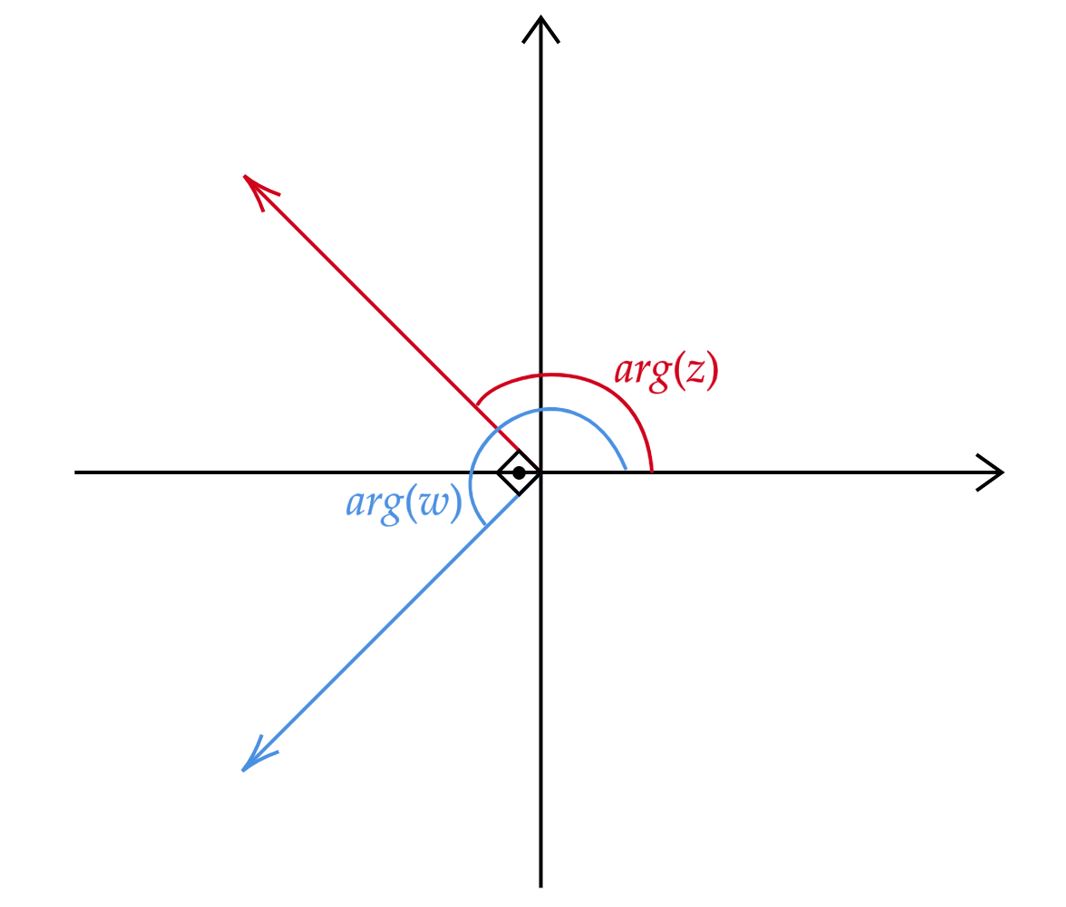

Ampliar Imagem

