Represente graficamente a função:
CossenoGPT
Teste
gratuitamente agora
mesmo! 
$F(\theta) = \frac{1}{1+\sin^{2} \theta}+ \frac{1}{1+\cos^{2} \theta}+ \frac{1}{1+\sec^{2} \theta}+ \frac{1}{1+\csc^{2} \theta}$, temos:
$F(\theta) = \frac{1}{1+\sin^{2} \theta}+ \frac{1}{1+\cos^{2} \theta}+ \frac{1}{1+\frac{1}{\cos^{2} \theta}}+\frac{1}{1+\frac{1}{\sin^{2} \theta}} = \frac{1}{1+\sin^{2} \theta}+ \frac{1}{1+\cos^{2} \theta}+ \frac{\cos^{2} \theta
}{1+\cos^{2} \theta}+ \frac{\sin^{2} \theta}{1+\sin^{2} \theta}$
Logo: $F(\theta) = (\frac{1}{1+\sin^{2} \theta}+\frac{\sin^{2} \theta}{1+\sin^{2} \theta})+(\frac{1}{1+\cos^{2} \theta}+\frac{\cos^{2} \theta}{1+\cos^{2} \theta})$ $=$ $2$, $\forall$ $\theta \neq \frac{k\pi}{2}$, $k\in \mathbb{Z}$
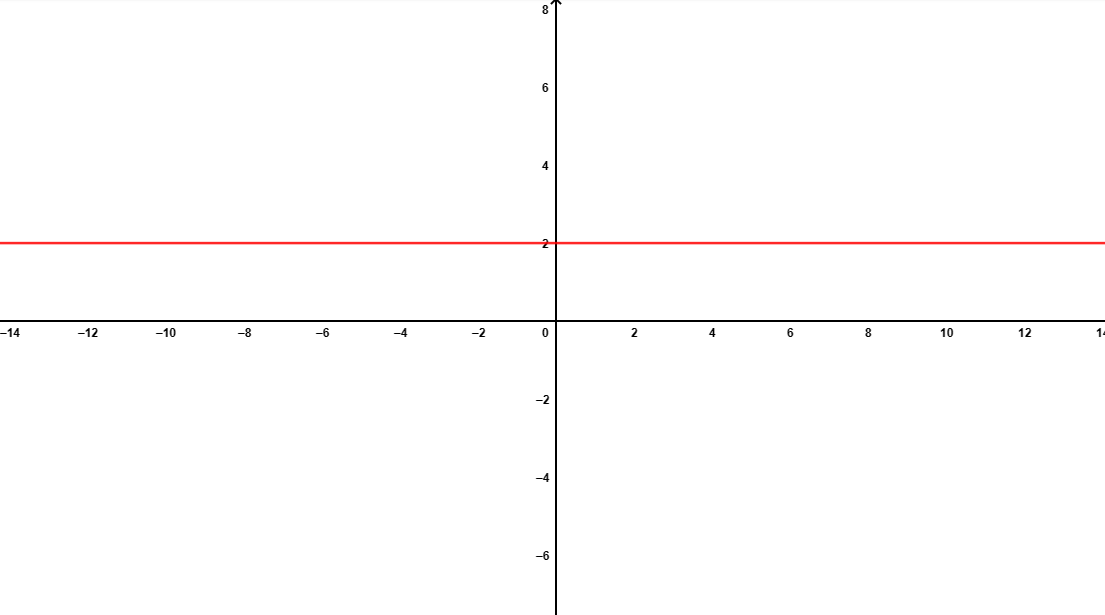
Enfim, obtém-se: $\boxed {F(\theta)=2}$, para todo $\theta$ não múltiplo de $\frac{\pi}{2}$. Então o gráfico de F é uma reta, paralela ao eixo das abcissas, que passa pelo ponto $(0,2)$.
Ampliar Imagem
21:54 02/03/2023
Está quase correto, observe apenas a condição de existência da secante e cossecante (múltiplos de noventa graus não podem fazer parte da solução)
08:35 03/03/2023
Isso, importante ressaltar que o gráfico ficaria com bolas abertas nos múltiplos de 90 (em vez de uma linha contínua)
