Uma escada de de comprimento está apoiada contra uma parede vertical com a sua extremidade inferior a da parede, como mostra a figura.
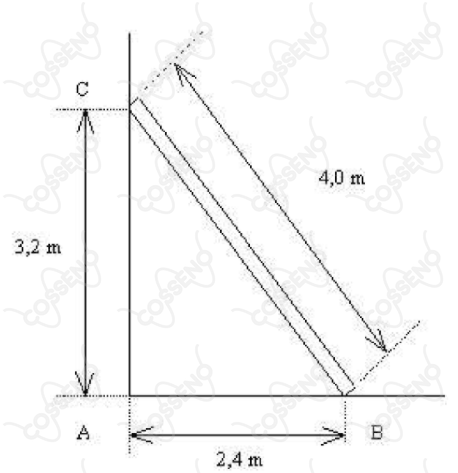
A escada pesa e seu centro de gravidade está localizado no ponto médio. Sabendo que os coeficientes de atrito estático entre a escada e o solo e entre a escada e a parede são, respectivamente, e , calcule:
a) a altura máxima, em relação ao solo, a que um homem de de peso pode subir, sem provocar o escorregamento da escada;
b) a distância máxima da parede a que se pode apoiar a parte inferior da escada vazia, sem provocar escorregamento.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Obrigado por solicitar a questão, Rafaela!
Começando pelo item A, vamos desenhar as forças aplicadas sobre a escada quando o homem está subindo:
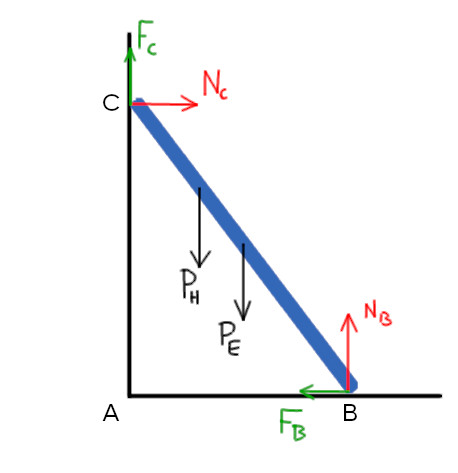 Para a escada permanecer em equilíbrio, a resultante das forças nas direções horizontal e vertical deve ser nula.
Portanto: $$\begin{cases}N_C = F_B\\ F_C + N_B = P_E + P_H\end{cases}$$
Como o módulo da força de atrito é dada por $F=\mu N$ e os pesos são conhecidos: $$\begin{cases}N_C = \mu_BN_B\\ \mu_CN_C + N_B = 20 + 90\end{cases}$$
Enfim, substituindo a primeira equação na segunda e inserindo os valor dos coeficientes de atrito: $$0{,}2\cdot0{,}5\cdot N_B + N_B = 110\\ N_B=\pu{100 Kgf}$$
E como $N_C = \mu_BN_B$, então $N_C=\pu{50 Kgf}$.
Além disso, para a escada permanecer em equilíbrio, o momento resultante deve ser nulo (soma dos torques é zero).
Portanto, atribuindo o ponto B como ponto de apoio: $$F_C\cdot 2{,}4 + N_C\cdot 3{,}2 = P_E\cdot 1{,}2 + P_H\cdot d$$
Sendo $d$ a distância horizontal entre o homem e o pé da escada, conforme mostrado na imagem:
Para a escada permanecer em equilíbrio, a resultante das forças nas direções horizontal e vertical deve ser nula.
Portanto: $$\begin{cases}N_C = F_B\\ F_C + N_B = P_E + P_H\end{cases}$$
Como o módulo da força de atrito é dada por $F=\mu N$ e os pesos são conhecidos: $$\begin{cases}N_C = \mu_BN_B\\ \mu_CN_C + N_B = 20 + 90\end{cases}$$
Enfim, substituindo a primeira equação na segunda e inserindo os valor dos coeficientes de atrito: $$0{,}2\cdot0{,}5\cdot N_B + N_B = 110\\ N_B=\pu{100 Kgf}$$
E como $N_C = \mu_BN_B$, então $N_C=\pu{50 Kgf}$.
Além disso, para a escada permanecer em equilíbrio, o momento resultante deve ser nulo (soma dos torques é zero).
Portanto, atribuindo o ponto B como ponto de apoio: $$F_C\cdot 2{,}4 + N_C\cdot 3{,}2 = P_E\cdot 1{,}2 + P_H\cdot d$$
Sendo $d$ a distância horizontal entre o homem e o pé da escada, conforme mostrado na imagem:
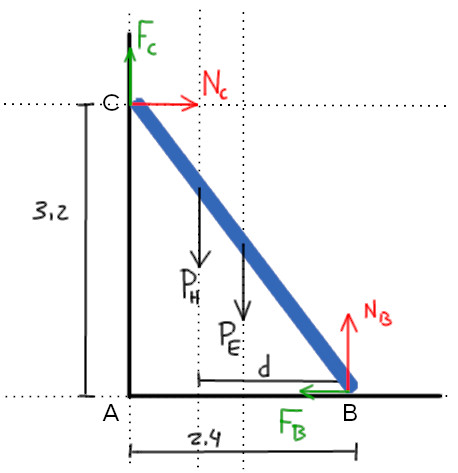 Assim, desenvolvendo a equação, chegamos a: $$0{,}2\cdot50 \cdot 2{,}4 + 50\cdot 3{,}2 = 20\cdot 1{,}2 + 90\cdot d\\\boxed{d=\dfrac{16}{9}\ m}$$
E então, por semelhança de triângulos, podemos calcular a altura $h$ do homem em relação ao solo.
Se o triângulo maior tem razão altura/base igual a $3{,}2/2{,}4=4/3$, então a razão $h/d$ também deverá ser a mesma: $$\dfrac{h}{\frac{16}{9}}=\dfrac{4}{3}\\\, \\ \boxed{h\simeq\pu{2,37 m}}$$
Já no item B, basta fazer o equilíbrio das forças sem o peso do homem: $$\begin{cases}N_C = F_B\\ F_C + N_B = P_E\end{cases}$$
De modo que $$\begin{cases}N_B = \pu{\dfrac{900}{11} Kgf}\\\,\\ N_C = \pu{\dfrac{450}{11} Kgf}\end{cases}$$
E o equilíbrio dos momentos agora terá os braços das forças como incógnitas:
Assim, desenvolvendo a equação, chegamos a: $$0{,}2\cdot50 \cdot 2{,}4 + 50\cdot 3{,}2 = 20\cdot 1{,}2 + 90\cdot d\\\boxed{d=\dfrac{16}{9}\ m}$$
E então, por semelhança de triângulos, podemos calcular a altura $h$ do homem em relação ao solo.
Se o triângulo maior tem razão altura/base igual a $3{,}2/2{,}4=4/3$, então a razão $h/d$ também deverá ser a mesma: $$\dfrac{h}{\frac{16}{9}}=\dfrac{4}{3}\\\, \\ \boxed{h\simeq\pu{2,37 m}}$$
Já no item B, basta fazer o equilíbrio das forças sem o peso do homem: $$\begin{cases}N_C = F_B\\ F_C + N_B = P_E\end{cases}$$
De modo que $$\begin{cases}N_B = \pu{\dfrac{900}{11} Kgf}\\\,\\ N_C = \pu{\dfrac{450}{11} Kgf}\end{cases}$$
E o equilíbrio dos momentos agora terá os braços das forças como incógnitas:
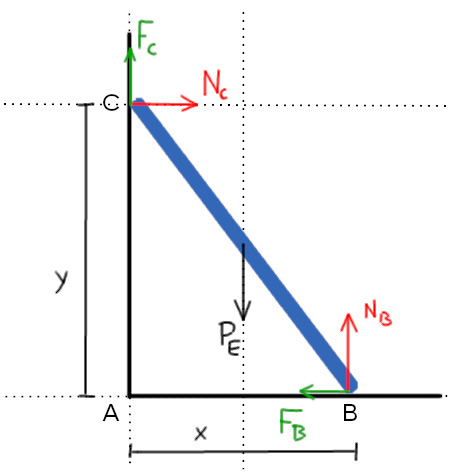 Portanto, atribuindo o ponto B como ponto de apoio: $$\begin{align*}F_C\cdot x + N_C\cdot y &= P_E\cdot \dfrac{x}{2}\\ \mu_CN_C\cdot x + N_C\cdot y &= P_E\cdot \dfrac{x}{2}\\ 0{,}2\cdot\dfrac{450}{11}\cdot x + \dfrac{450}{11}\cdot y &= 90\cdot \dfrac{x}{2}\\ y&=0{,}9x\end{align*}$$
E como a escada forma um triângulo retângulo de catetos $x$, $y$ e hipotenusa $\pu{4 m}$, podemos aplicar o teorema de Pitágoras para obter o comprimento pedido $x$: $$4^2=x^2 + \left(0{,}9x\right)^2\\\,\\ x=\pu{\dfrac{40}{\sqrt{181}} m}\\\,\\\boxed{x\simeq\pu{2,97 m}}$$
Qualquer dúvida é só perguntar aqui embaixo na seção de comentários, bons estudos! 🚀
Portanto, atribuindo o ponto B como ponto de apoio: $$\begin{align*}F_C\cdot x + N_C\cdot y &= P_E\cdot \dfrac{x}{2}\\ \mu_CN_C\cdot x + N_C\cdot y &= P_E\cdot \dfrac{x}{2}\\ 0{,}2\cdot\dfrac{450}{11}\cdot x + \dfrac{450}{11}\cdot y &= 90\cdot \dfrac{x}{2}\\ y&=0{,}9x\end{align*}$$
E como a escada forma um triângulo retângulo de catetos $x$, $y$ e hipotenusa $\pu{4 m}$, podemos aplicar o teorema de Pitágoras para obter o comprimento pedido $x$: $$4^2=x^2 + \left(0{,}9x\right)^2\\\,\\ x=\pu{\dfrac{40}{\sqrt{181}} m}\\\,\\\boxed{x\simeq\pu{2,97 m}}$$
Qualquer dúvida é só perguntar aqui embaixo na seção de comentários, bons estudos! 🚀

Ampliar Imagem

Ampliar Imagem

Ampliar Imagem

13:45 18/02/2023
Muitíssimo obrigada pela resolução, entendi plenamente! Perdoe a demora para agradecer.

