Na figura abaixo, uma corda é fixada a uma parede e depois de passar por uma roldana é tensionada por uma esfera metálica com de massa. Uma segunda esfera metálica, firmemente presa ao solo, é colocada verticalmente abaixo da primeira.
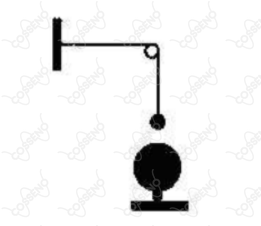
Sabendo que a distância entre a parede e a roldana é de e que a distância entre os centros das esferas é de , determine a frequência de ressonância do trecho da corda entre a parede e a roldana:
a) Com duas esferas descarregadas;
b) Com as duas esferas carregadas, a primeira com uma carga elétrica de e a segunda com uma carga elétrica de .
Dados:
aceleração da gravidade: $g=9{,}8\ m/s^2$
permissividade do vácuo: $\varepsilon_0=8{,}9\times 10^{-2}\ F/m$
densidade linear da corda: $\mu=2{,}0\ g/m$
aceleração da gravidade: $g=9{,}8\ m/s^2$
permissividade do vácuo: $\varepsilon_0=8{,}9\times 10^{-2}\ F/m$
densidade linear da corda: $\mu=2{,}0\ g/m$
$-$ A priori, por frequência de ressonância, entende-se como frequência fundamental, isto é, temos a expressão: $L = \lambda/2$
$• \ \text{Alternativa (a):}$ Com as duas esferas descarregadas, têm-se que a tração seja igual ao peso da esfera menor, assim, com conhecimento da $\text{Equação de Taylor}$, temos:
\begin{matrix} T = \large{\sqrt{ \frac{V}{\mu} }} &,& \color{royalblue}{V = \lambda \ .\ f = 2L \ .\ f } &\Rightarrow& \fbox{$V = f$}
\end{matrix} Continuando, \begin{matrix} 3,3 = \large{\sqrt{ \frac{f}{\mu} }} &,& \color{royalblue}{\mu = 2 \ g/m = 2.10^{-3} \ kg/m }&\Rightarrow& \fbox{$f \cong 40,2 \ Hz$}
\end{matrix}
$• \ \text{Alternativa (b):}$ Agora, com a presença de cargas nas esferas, teremos uma maior tração, a qual equacionamos como:
\begin{matrix} T = P + |F_e| &,& F_e = 0,18 &\Rightarrow& T \cong 3,41 \ N
\end{matrix} Analogamente, \begin{matrix} 3,41 = \large{\sqrt{ \frac{f}{\mu} }} &\Rightarrow& \fbox{$f \cong 41,3 \ Hz$}
\end{matrix}
