Na figura abaixo, a partícula , que se encontra em queda livre, passa pelo primeiro máximo de interferência com velocidade de e, após um segundo, atinge o máximo central. A fonte de luz é monocromática com comprimento de onda de Angstroms e a distância entre os centros da fenda dupla é igual a . Calcule a distância .
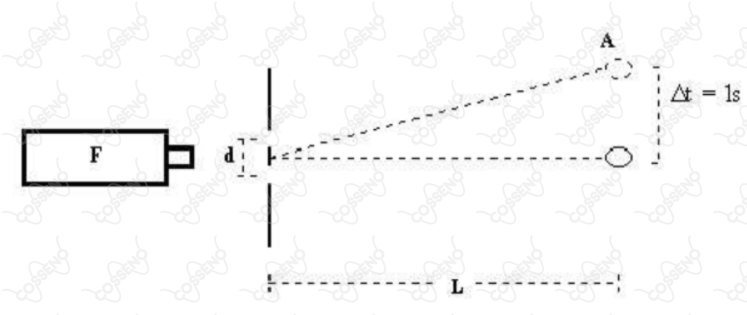
aceleração da gravidade $=10\ m/s^2$
$-$ Podemos esboçar a situação como abaixo, nela, sabemos que $\Delta y$ é a distância entre o máximo central e o primeiro máximo, determinaremos essa distância usando cinemática. Todavia, faremos antes uma suposição necessária, isto é, admitir que $L$ seja suficientemente grande para o $\sin{\alpha} \cong \tan{\alpha}$, assim, podemos escrever:
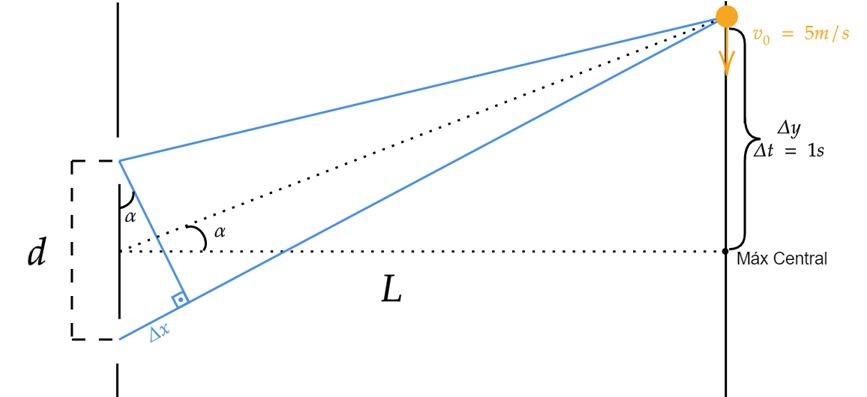\begin{matrix} \sin{\alpha} = \tan{\alpha} &\Rightarrow& \large{ \frac{\Delta x}{d} = \frac{\Delta y}{L} }
\end{matrix}
$-$ Como o enunciado fornece a informação da partícula estar, a priori, em seu primeiro máximo, temos:
\begin{matrix} \Delta x = N.\frac{\lambda}{2} &,& \text{primeiro máximo:} \ \ N = 2 &\Rightarrow& \fbox{$\Delta x = \lambda$}
\end{matrix}
$-$ Agora, usando as equações da cinemática de um $\text{MUV}$:
\begin{matrix} \Delta y = v_0.\Delta t + a.\frac{\Delta t^2}{2} &\Rightarrow & \fbox{$\Delta y = 5 \ m$} \end{matrix}
$-$ Portanto, substituindo os nossos resultados na primeira equação que formulamos, têm-se:
\begin{matrix} L = \large{\frac{d.\Delta y}{\lambda}} &\Rightarrow& \fbox{$L = 20 \ m$}
\end{matrix}
$\color{orangered}{Obs:}$ $1Å = 10^{-10}m$
Ampliar Imagem
