Uma mesa giratória tem velocidade angular constante , em torno do eixo . Sobre esta mesa encontram-se dois blocos, de massas e , ligados por uma corda inelástica que passa por uma roldana fixa à mesa, conforme a figura abaixo.
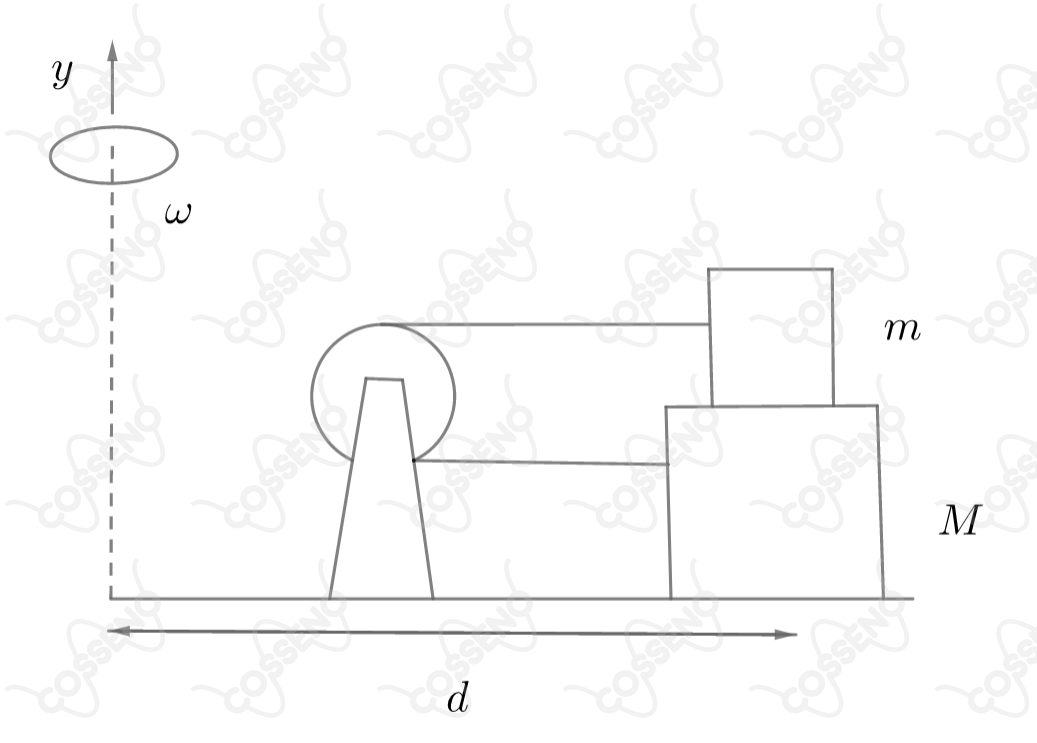
Considerando que não existe atrito entre a mesa e o bloco , determine o coeficiente de atrito mínimo entre os dois blocos para que não haja movimento relativo entre eles.
Considere $d$ a distância dos blocos ao eixo de rotação.
Despreze as massas da roldana e da corda.
Despreze as massas da roldana e da corda.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pelas dimensões dos blocos na imagem, convém assumir que $M >m$. Nessa perspectiva, não é difícil perceber que a tração que puxa o bloco menor, é exatamente igual àquela que puxa o maior - vínculo geométrico. Com isso, analisando as forças que atuam em cada bloco:
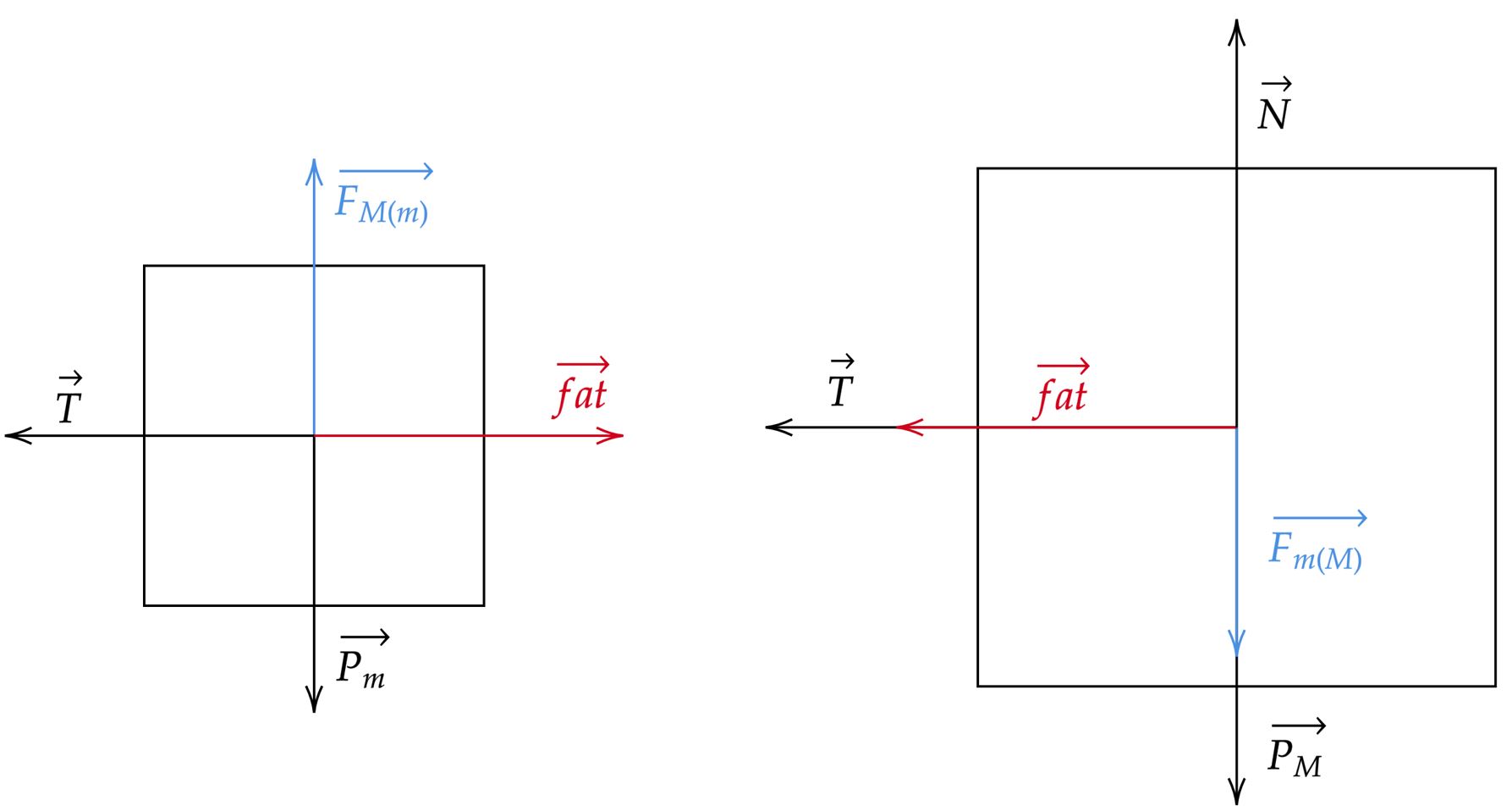 Note que a "inércia" do bloco de massa $M$ é maior, o bloco em cima dele tende a escapar para dentro da curva, visto o que supomos no início. Desse modo, têm-se: \begin{matrix}\text{eixo x:}&
\begin{cases}m \cdot \omega^2 \cdot d = T - fat \\ M \cdot \omega^2 \cdot d = T + fat
\end{cases} &\Rightarrow& \omega^2 \cdot d \cdot (M-m) = 2fat & (1)
\end{matrix}Continuando,\begin{matrix} |\vec{F_{m(M)}}| = |\vec{F_{M(m)}}| = F &|& fat = \mu \cdot F
\end{matrix}Assim, pelo bloco menor,\begin{matrix}\text{eixo y:}&
\begin{cases} F = m g
\end{cases} &\overset{(1)}{\Rightarrow}& \omega^2 \cdot d \cdot (M-m) = 2\mu (m g) &\therefore&
\mu = \dfrac{(M-m)\omega^2 d}{2mg} &\tiny{\blacksquare}
\end{matrix}
Note que a "inércia" do bloco de massa $M$ é maior, o bloco em cima dele tende a escapar para dentro da curva, visto o que supomos no início. Desse modo, têm-se: \begin{matrix}\text{eixo x:}&
\begin{cases}m \cdot \omega^2 \cdot d = T - fat \\ M \cdot \omega^2 \cdot d = T + fat
\end{cases} &\Rightarrow& \omega^2 \cdot d \cdot (M-m) = 2fat & (1)
\end{matrix}Continuando,\begin{matrix} |\vec{F_{m(M)}}| = |\vec{F_{M(m)}}| = F &|& fat = \mu \cdot F
\end{matrix}Assim, pelo bloco menor,\begin{matrix}\text{eixo y:}&
\begin{cases} F = m g
\end{cases} &\overset{(1)}{\Rightarrow}& \omega^2 \cdot d \cdot (M-m) = 2\mu (m g) &\therefore&
\mu = \dfrac{(M-m)\omega^2 d}{2mg} &\tiny{\blacksquare}
\end{matrix}

Ampliar Imagem

