De dois pontos e situados sobre a mesma vertical, respectivamente, a metros e metros do solo, deixa-se cair no mesmo instante duas esferas conforme mostra a figura abaixo. Uma prancha se desloca no solo, horizontalmente, com movimento uniforme. As esferas atingem a prancha em pontos que distam metros.
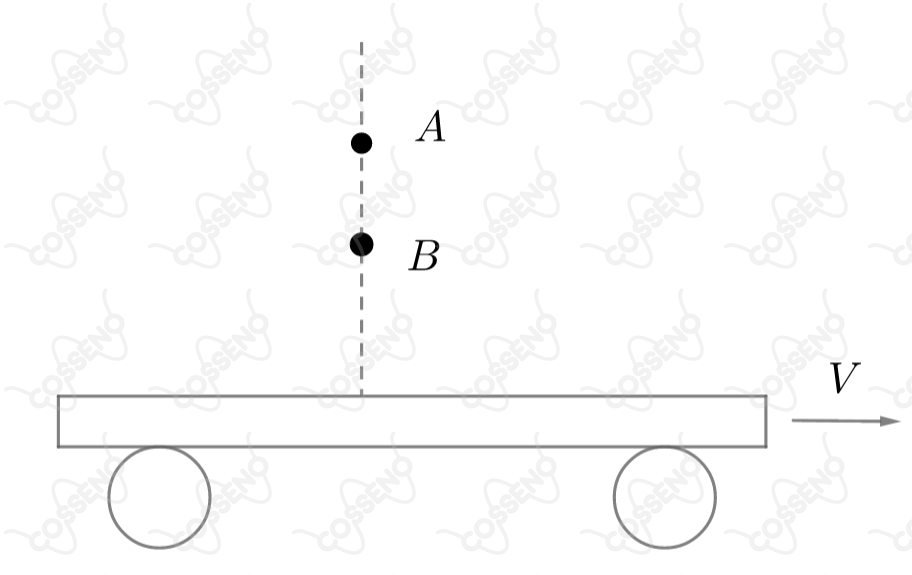
Supondo a aceleração local da gravidade igual a e desprezando a resistência do ar, determine a velocidade da prancha.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$-$ Repare que, o intervalo de tempo entre $B$ e $A$ tocarem a prancha é justamente o intervalo de tempo que a prancha percorre $2m$. Desse modo, se o tempo de queda de $B$ for $\Delta t_1$, o de $A$ for $\Delta t_2$, teremos: \begin{matrix} \Delta t_2 - \Delta t_1 = \Delta t_3 &,& \Delta t_3: \ \text{tempo que a prancha percorre 2 metros}
\end{matrix}Com isso, sabe-se que tanto o movimento de $A$ como de $B$ são retilíneos e uniformemente acelerados, assim, pela lei horária do movimento:\begin{matrix}
B: & \underbrace{\Delta y_B}_{20m} = \underbrace{v_{0_B}}_{0}\Delta t_1 + g {\large{(\frac{\Delta t^2_1}{2})}} &\Rightarrow& \Delta t_1^2 =4 &\therefore& \Delta t_1 = 2 \ s \\ \\
A: & \underbrace{\Delta y_A}_{45m} = \underbrace{v_{0_A}}_{0}\Delta t_2 + g {\large{(\frac{\Delta t^2_2}{2})}} &\Rightarrow& \Delta t_2^2 =9 &\therefore& \Delta t_2 = 3 \ s
\end{matrix}Conforme resultados anteriores: \begin{matrix} \Delta t_3 = 1 \ s &\Rightarrow& {\Large{\frac{2}{V}}} = 1 &\therefore& V = 2 \ m/s &\tiny{\blacksquare}
\end{matrix}

