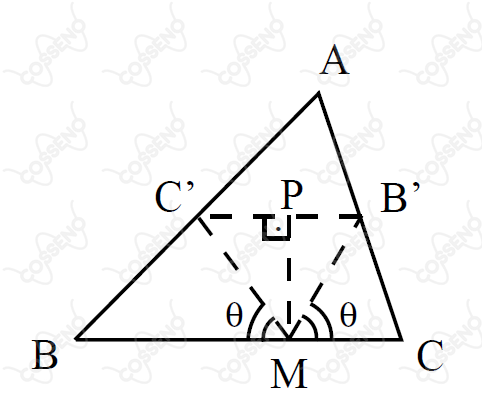
Seja um triângulo qualquer. Por e pontos médios dos lados e , respectivamente, traçam-se duas retas que se cortam em um ponto , situado sobre o lado , e que fazem com esse lado ângulos iguais conforme a figura abaixo. Demonstre que:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$-$ A priori, com conhecimento dos ângulos alternos internos, temos que $MC^{′}B^{′}$ é isósceles. Ademais, sabida as propriedades da base média, se $\overline{BC} = 2a$, então $\overline{C^{′}B^{′}} = a$, nesse viés, denotemos $\overline{PM} = h$, veja que pelo triângulo $MC^{′}B^{′}$: \begin{matrix} \cot{\theta} &=& \large{\frac{a}{2h}}
\end{matrix}$-$ Agora, tracemos duas perpendiculares, a primeira de $C^{′}$ até o lado $\overline{BM}$ no ponto $D$, já a segunda de $B^{′}$ até o lado $\overline{MC}$ no ponto $E$. Atente que, antes de trabalharmos essas alturas relativas, devemos definir algumas coisas a partir do ponto $M$, siga o raciocínio: \begin{matrix}
\overline{C^{′}B^{′}} = \overline{DE} = a &\Rightarrow& \overline{BD} = y &\Longleftrightarrow& \overline{CE} = a - y
\end{matrix}Além disso, não é difícil perceber que as duas perpendiculares são iguais a $\overline{PM}$, ou seja, iguais a $h$. Com isso, analisando os dois triângulos retângulos formados, temos: \begin{matrix}
\cot{B} &=& \large{\frac{\overline{BD}}{h}} &=& \large{\frac{y}{h}} &&,&& \cot{C} &=& \large{\frac{\overline{CE}}{h}} &=& \large{\frac{a -y}{h}}
\end{matrix}Com isso, \begin{matrix} \cot{B} + \cot{C} &=& \large{\frac{a}{h}}
\end{matrix}Portanto, \begin{matrix} \cot{\theta} &=& \frac{1}{2} \ . \ (\cot{B} + \cot{C} ) &=& \large{\frac{a}{2h}} & \tiny{\blacksquare}
\end{matrix}

