Um míssil viajando paralelamente à superfície da terra com uma velocidade de passa sobre um canhão à altura de no exato momento em que seu combustível acaba. Neste instante, o canhão dispara a e atinge o míssil. O canhão está no topo de uma colina de de altura.
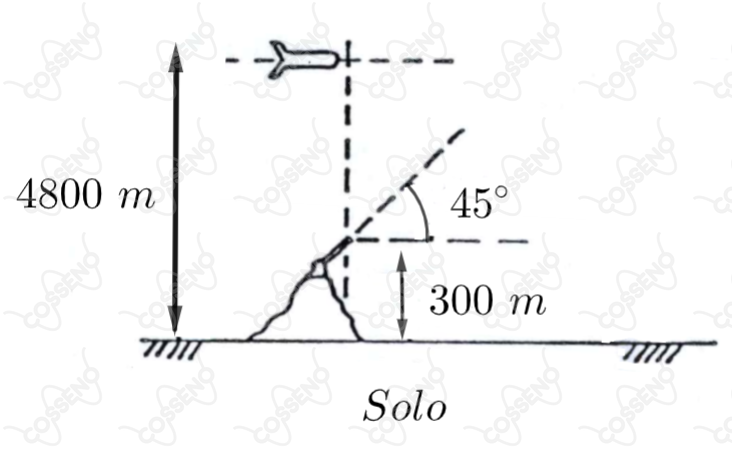
Sabendo-se que a aceleração local da gravidade , determine a altura da posição de encontro do míssil com a bala do canhão, em relação ao solo. Despreze a resistência do ar.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$-$ Num plano cartesiano, a situação pode ser esboçada como:
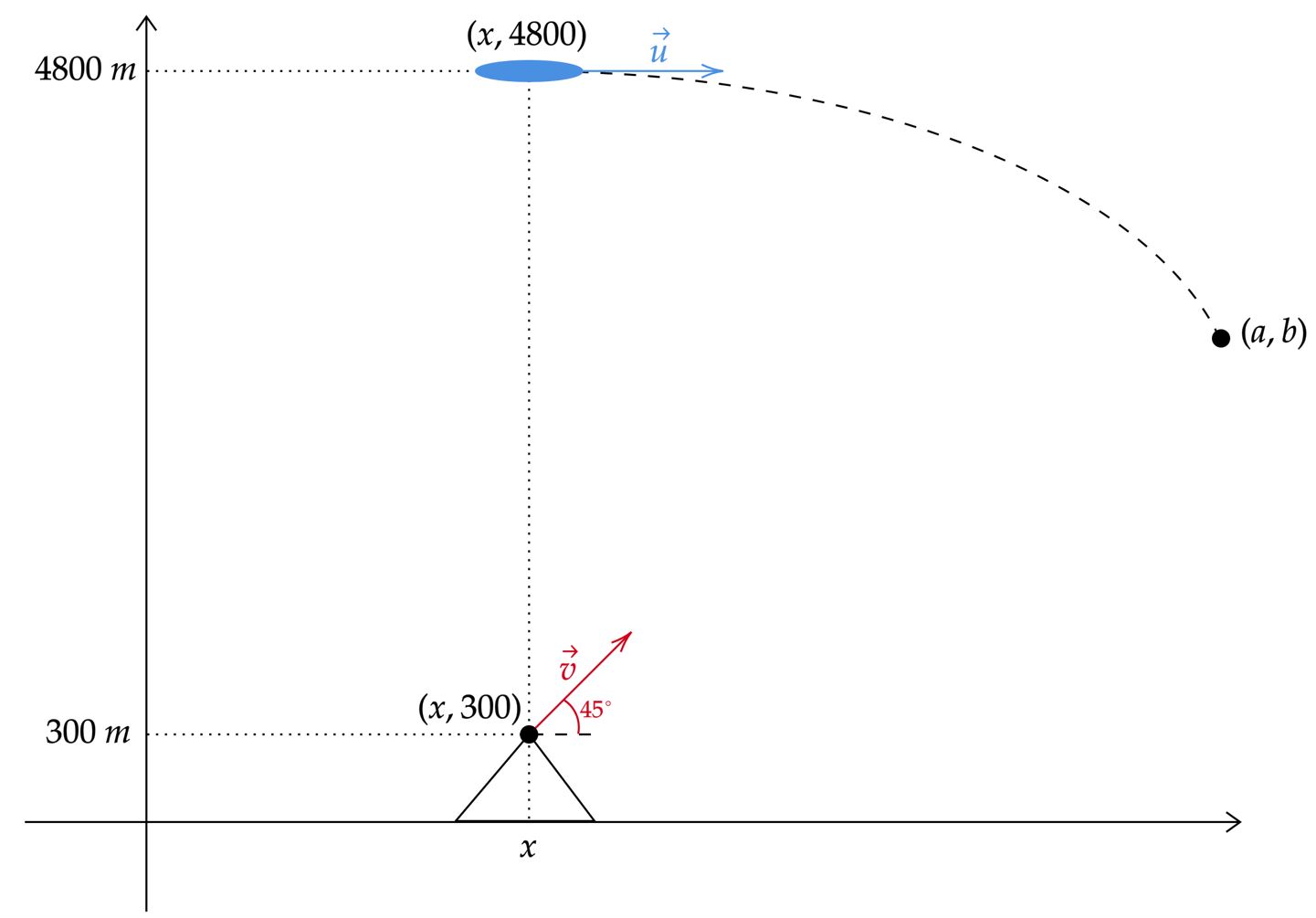 Pelo esboço acima, entende-se que a colisão do míssil com a bala do canhão será em $(a,b)$. Além disso, sabemos que o deslocamento horizontal de ambos - bala e míssil - é retilíneo e uniforme, logo, pensando na distância até o encontro, têm-se: \begin{matrix} a - x = v_x \cdot \Delta t &,& a- x = u \cdot \Delta t &\Rightarrow& v_x = u&|& v_x = v_{y_0} = u = 180 \ m/s
\end{matrix}Com isso, podemos agora analisar o movimento retilíneo e uniformemente acelerado no eixo $y$, escrevendo a lei horária de cada um, temos:\begin{matrix} \text{Míssil:} & y(t) = y(0) + u_{y_0}t- g {\large{(\frac{t^2}{2})}} &\Rightarrow& y(t) =4800- g {\large{(\frac{t^2}{2})}} \\ \\
\text{Bala:} & y_1(t) = y_1(0) + v_{y_0}t - g {\large{(\frac{t^2}{2})}} &\Rightarrow& y_1(t) =300 + 180 t- g {\large{(\frac{t^2}{2})}}
\end{matrix}Atente que, $u_{y_0}$ é o módulo da velocidade inicial com que o míssil caí, no caso, nula. Analogamente, $v_{y_0}$ é o módulo da velocidade inicial da bala no eixo $y$, desse modo, podemos definir o encontro como: \begin{matrix} b = y(t) = y_1(t) &\Rightarrow& 4800 = 300 + 180t &\therefore& t = 25s
\end{matrix}Conhecido o intervalo de tempo até a colisão, basta substituir em qualquer uma das leis horárias, assim: \begin{matrix} y(25) = b = 4800 - 10{\large{(\frac{25^2}{2})}} &\therefore& b = 1675 \ m & \tiny{\blacksquare}
\end{matrix}
Pelo esboço acima, entende-se que a colisão do míssil com a bala do canhão será em $(a,b)$. Além disso, sabemos que o deslocamento horizontal de ambos - bala e míssil - é retilíneo e uniforme, logo, pensando na distância até o encontro, têm-se: \begin{matrix} a - x = v_x \cdot \Delta t &,& a- x = u \cdot \Delta t &\Rightarrow& v_x = u&|& v_x = v_{y_0} = u = 180 \ m/s
\end{matrix}Com isso, podemos agora analisar o movimento retilíneo e uniformemente acelerado no eixo $y$, escrevendo a lei horária de cada um, temos:\begin{matrix} \text{Míssil:} & y(t) = y(0) + u_{y_0}t- g {\large{(\frac{t^2}{2})}} &\Rightarrow& y(t) =4800- g {\large{(\frac{t^2}{2})}} \\ \\
\text{Bala:} & y_1(t) = y_1(0) + v_{y_0}t - g {\large{(\frac{t^2}{2})}} &\Rightarrow& y_1(t) =300 + 180 t- g {\large{(\frac{t^2}{2})}}
\end{matrix}Atente que, $u_{y_0}$ é o módulo da velocidade inicial com que o míssil caí, no caso, nula. Analogamente, $v_{y_0}$ é o módulo da velocidade inicial da bala no eixo $y$, desse modo, podemos definir o encontro como: \begin{matrix} b = y(t) = y_1(t) &\Rightarrow& 4800 = 300 + 180t &\therefore& t = 25s
\end{matrix}Conhecido o intervalo de tempo até a colisão, basta substituir em qualquer uma das leis horárias, assim: \begin{matrix} y(25) = b = 4800 - 10{\large{(\frac{25^2}{2})}} &\therefore& b = 1675 \ m & \tiny{\blacksquare}
\end{matrix}

Ampliar Imagem

