Pretende-se colocar ar sob pressão em um reservatório de volume . A operação se faz isotermicamente.
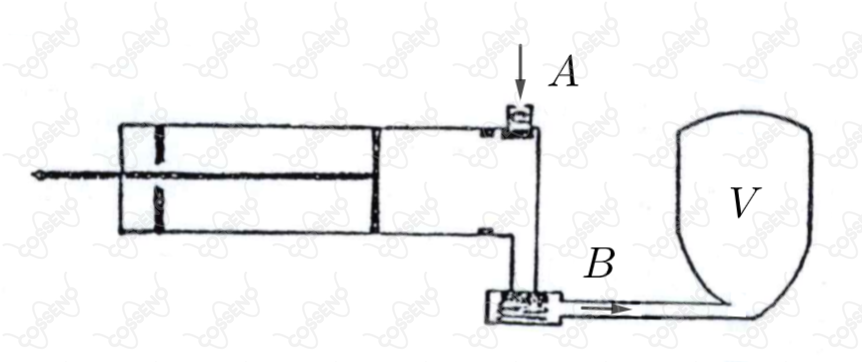
Utiliza-se uma bomba mostrada na figura onde as válvulas e impedem fluxo do ar em sentido inverso ao indicado pelas setas. O volume da bomba descomprimida (a pressão atmosférica) é .
a) Estando inicialmente o reservatório na pressão atmosférica, determine a expressão da pressão absoluta no reservatório após compressões da bomba;
b) Voltando à condição inicial, considere agora a operação como adiabática e determine a expressão da pressão absoluta no reservatório após compressões da bomba.
Obs: Dê as respostas em função das variáveis $P_{atm}$
$V$
$V_0$
$N$ e $\gamma$. Considere o ar como gás perfeito.
$V$
$V_0$
$N$ e $\gamma$. Considere o ar como gás perfeito.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$a)$ Vamos analisar o que acontece com a pressão numa etapa genérica. Ou seja, a pressão do reservatória sendo $p_k$, vamos determinar a expressão da pressão $p_{k+1}$ (pressão após a $k$-ésima compressão da bomba). Observe que o único fator que interfere na mudança da pressão é o aumento da quantidade de gás, ou seja do número de mols, pois tanto a temperatura, quanto o volumo, no reservatório, são constantes. Então, temos no reservatório: $$p_k \cdot V = n_k \cdot R \cdot T$$sendo $n_k$ o número de mols que também muda para cada bombeada.
A quantidade de gás que será inserida no reservatório pode ser encontrada analisando a bomba: quando a bomba é enchida do gás externo, que está em pressão atmosférica, temos que $$P_{atm} \cdot V_0 = n_{inserido} \cdot R \cdot T$$Observe que $n_{inserido}$ é sempre o mesmo em todas as etapas, pois as demais variáveis são sempre constantes.
Em sequência, tal quantidade de gás será toda bombeada para dentro do reservatório, que terá após a $k$-ésima bombeada $n_k + n_{inserido}$ mols. Assim: $$p_{k+1} \cdot V = (n_k + n_{inserido})\cdot R \cdot T$$Usando as duas equações anteriores: $$p_{k+1}V = p_kV + P_{atm}V_0 \Rightarrow p_{k+1} = p_k + P_{atm}\cdot \dfrac{V_0}{V}$$Ou seja, a cada bombeada, a pressão é acrescida de um valor fixo, ou seja, as pressões estão em P.A. Logo, após $N$ bombeadas: $$P_{N+1} = P_{inicial} + N \cdot P_{atm} \cdot \dfrac{V_0}{V} = P_{atm} \bigg(1 + N\dfrac{V_0}{V}\bigg)$$

