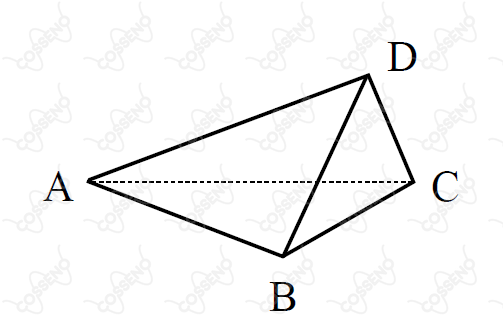
Na exploração de uma mina foi feito o corte indicado na figura abaixo. Para calcular o volume do minério extraído do corte, foram medidos: , é perpendicular ao plano , e . Calcule este volume.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

O poliedro do problema é uma pirâmide de base triangular (tetraedro). Lembrando que o volume da pirâmide é $V=A_b\cdot h/3$ (um terço da área da base vezes altura), já podemos identificar que a altura é $\overline{CD}$ e a base é o triângulo $\text{ABC}$. Com os passos a seguir iremos determinar a área do triângulo $\text{ABC}$.
Primeiro, para determinar o comprimento de cada aresta, vamos analisar as faces do tetraedro individualmente. Assim, poderemos aplicar relações trigonométricas em cada triângulo.
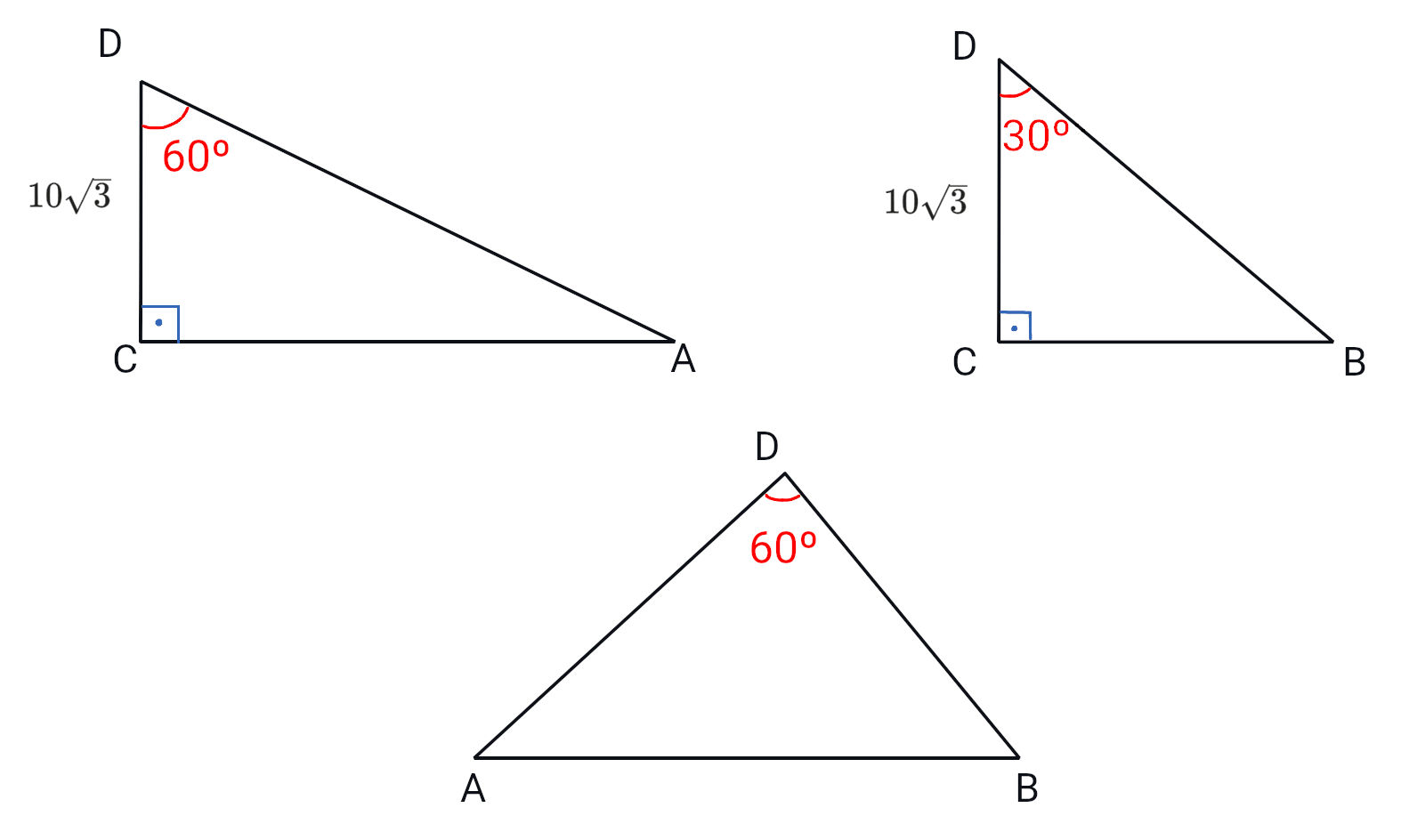 Começando com o triângulo $\text{ACD}$: $$\begin{align}\overline{CD}&=10\sqrt{3}\ \pu{dm}\\ \\\overline{AD}&=\dfrac{\overline{CD}}{\cos{60^\circ}}=20\sqrt{3}\ \pu{dm}\\\\ \overline{AC}&=\overline{CD}\cdot\tan{60^\circ}=\pu{30 dm}\end{align}$$
Analogamente, para o triângulo $\text{BCD}$: $$\begin{align}\overline{CD}&=10\sqrt{3}\ \pu{dm}\\ \\\overline{BD}&=\pu{20 dm}\\\\ \overline{BC}&=\pu{10 dm}\end{align}$$
Enfim, para o triângulo $\text{ABD}$, podemos aplicar a lei dos cossenos: $$\overline{AB}^2=\overline{AD}^2+\overline{DB}^2-2\cdot \overline{AD}\cdot \overline{DB}\cos{60^\circ}$$Como já calculamos $\overline{AD}$ e $\overline{DB}$ nos passos anteriores: $$\overline{AB}^2=(20\sqrt{3})^2+20^2-2\cdot20\sqrt{3}\cdot20\cdot\cos{60^\circ}\\\overline{AB}=20\sqrt{4-\sqrt{3}}\ \pu{dm}$$
Portanto, os lados do triângulo \text{ABC} (base da pirâmide) são: $$\begin{align}\overline{AB}&=20\sqrt{4-\sqrt{3}}\ \pu{dm}\\\overline{BC}&=\pu{10 dm}\\\overline{AC}&=\pu{30 dm}\end{align}$$
Para calcular a área desse triângulo, recorremos à fórmula de Heron: $$A_b=\sqrt{p(p-a)(p-b)(p-c)}$$ sendo $p=\dfrac{\overline{AB}+\overline{AC}+\overline{BC}}{2}$ o semiperímetro do triângulo. Logo: $$A_b=100\sqrt{3\sqrt3 - 3}\ \pu{dm2}$$
Fazendo com que $$V=\dfrac{A_b\cdot \overline{CD}}{3}=\dfrac{100\sqrt{3\sqrt3 - 3}\cdot 10\sqrt{3}}{3}\\ \boxed{V=1000\sqrt{\sqrt{3}-1}\ \pu{dm3}}$$
Começando com o triângulo $\text{ACD}$: $$\begin{align}\overline{CD}&=10\sqrt{3}\ \pu{dm}\\ \\\overline{AD}&=\dfrac{\overline{CD}}{\cos{60^\circ}}=20\sqrt{3}\ \pu{dm}\\\\ \overline{AC}&=\overline{CD}\cdot\tan{60^\circ}=\pu{30 dm}\end{align}$$
Analogamente, para o triângulo $\text{BCD}$: $$\begin{align}\overline{CD}&=10\sqrt{3}\ \pu{dm}\\ \\\overline{BD}&=\pu{20 dm}\\\\ \overline{BC}&=\pu{10 dm}\end{align}$$
Enfim, para o triângulo $\text{ABD}$, podemos aplicar a lei dos cossenos: $$\overline{AB}^2=\overline{AD}^2+\overline{DB}^2-2\cdot \overline{AD}\cdot \overline{DB}\cos{60^\circ}$$Como já calculamos $\overline{AD}$ e $\overline{DB}$ nos passos anteriores: $$\overline{AB}^2=(20\sqrt{3})^2+20^2-2\cdot20\sqrt{3}\cdot20\cdot\cos{60^\circ}\\\overline{AB}=20\sqrt{4-\sqrt{3}}\ \pu{dm}$$
Portanto, os lados do triângulo \text{ABC} (base da pirâmide) são: $$\begin{align}\overline{AB}&=20\sqrt{4-\sqrt{3}}\ \pu{dm}\\\overline{BC}&=\pu{10 dm}\\\overline{AC}&=\pu{30 dm}\end{align}$$
Para calcular a área desse triângulo, recorremos à fórmula de Heron: $$A_b=\sqrt{p(p-a)(p-b)(p-c)}$$ sendo $p=\dfrac{\overline{AB}+\overline{AC}+\overline{BC}}{2}$ o semiperímetro do triângulo. Logo: $$A_b=100\sqrt{3\sqrt3 - 3}\ \pu{dm2}$$
Fazendo com que $$V=\dfrac{A_b\cdot \overline{CD}}{3}=\dfrac{100\sqrt{3\sqrt3 - 3}\cdot 10\sqrt{3}}{3}\\ \boxed{V=1000\sqrt{\sqrt{3}-1}\ \pu{dm3}}$$

Ampliar Imagem

