Na figura abaixo, o bloco é um cubo de aresta e massa específica .
Sua face superior e esquerda está coberta por uma fina placa metálica de massa desprezível, paralela a uma placa quadrada , metálica, de lado , fixada na rampa, a uma distância do bloco, o qual oscila sem atrito sobre a rampa partindo da posição indicada na figura.
Sabendo que a aceleração da gravidade é , a permissividade do ar é e a capacitância mínima entre as placas é , determine a expressão literal da constante da mola (no instante da figura, a força da mola é nula).
$-$ Segundo enunciado, a capacitância deve ser mínima, isto é, a expressão: $C = \large{\frac{\epsilon \ . \ A}{d}}$ deve tender ao mínimo. Atente que, $\epsilon$ e $A$ são constantes, o que implica a necessidade de $d$ ser o maior possível. Nessa perspectiva, sabemos que $d>d_0$, pois a mola irá se comprimir $\Delta x$, sendo assim: $d - d_o =\Delta x$
Com isso, comecemos encontrando $\Delta x$, mas antes, repare na imagem que esboça a situação.
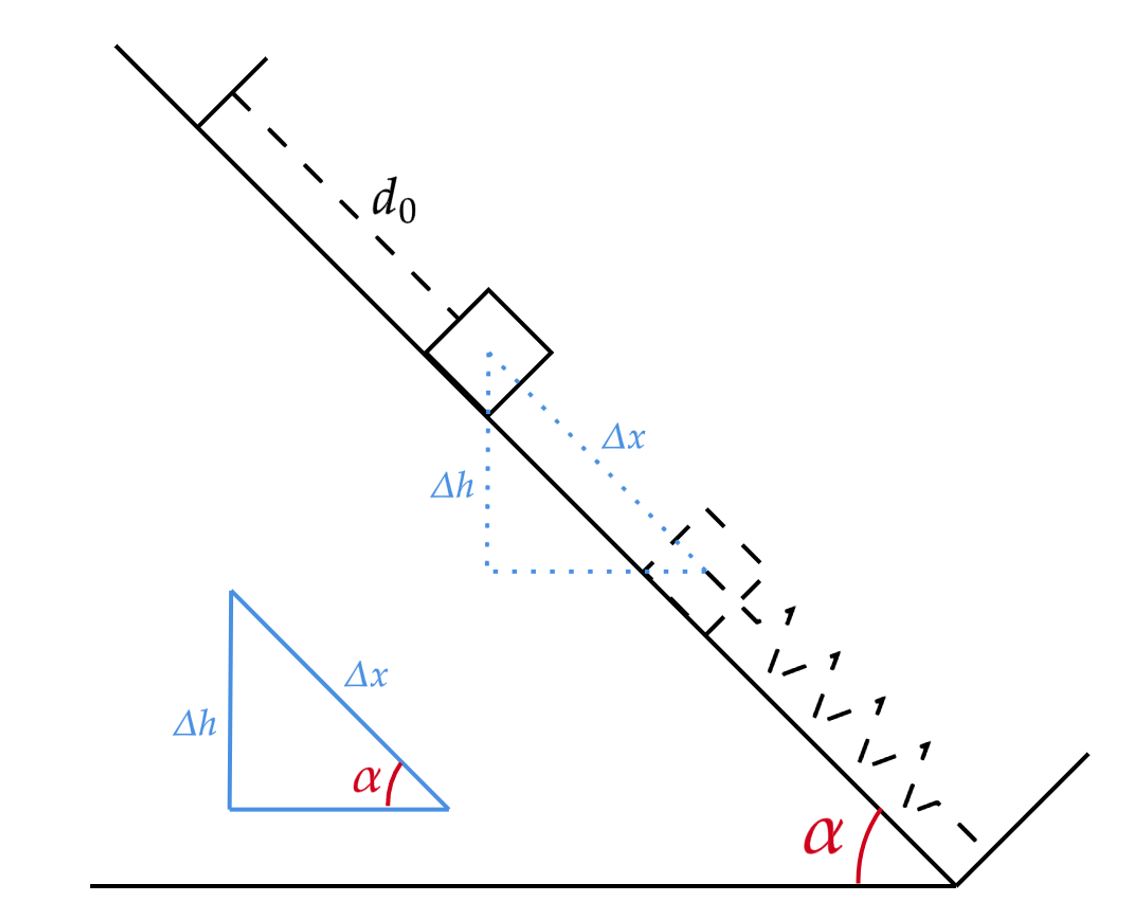Agora, pela conservação da energia mecânica, temos:
\begin{matrix} mg\Delta h = \large{\frac{K(\Delta x)^2}{2}} &\Rightarrow& K =\large{ \frac{2mg\sin{\alpha}}{\Delta x}} &\color{royalblue}{,}& \color{royalblue}{\Delta h = \Delta x\sin{\alpha}}
\end{matrix} Continuando, \begin{matrix}K =\large{ \frac{2mg\sin{\alpha}}{d - d_0}} &\Rightarrow& K =\large{ \frac{C(2mg\sin{\alpha})}{\epsilon_0 a^2- Cd_0}} &\color{royalblue}{,}& \color{royalblue}{C = \large{\frac{\epsilon_0 \ . \ a^2}{d}}}
\end{matrix}
Como $\rho = m/a^3$ \begin{matrix} & K =\Large{ \frac{C(2\rho a^3g\sin{\alpha})}{\epsilon_0 a^2- Cd_0}}
\end{matrix}
Ampliar Imagem
