$• \ \text{a)}$ $\color{royalblue}{\text{e = 0,8}}$ Pensando na situação descrita, pode-se esboçar o a sequência de eventos abaixo: 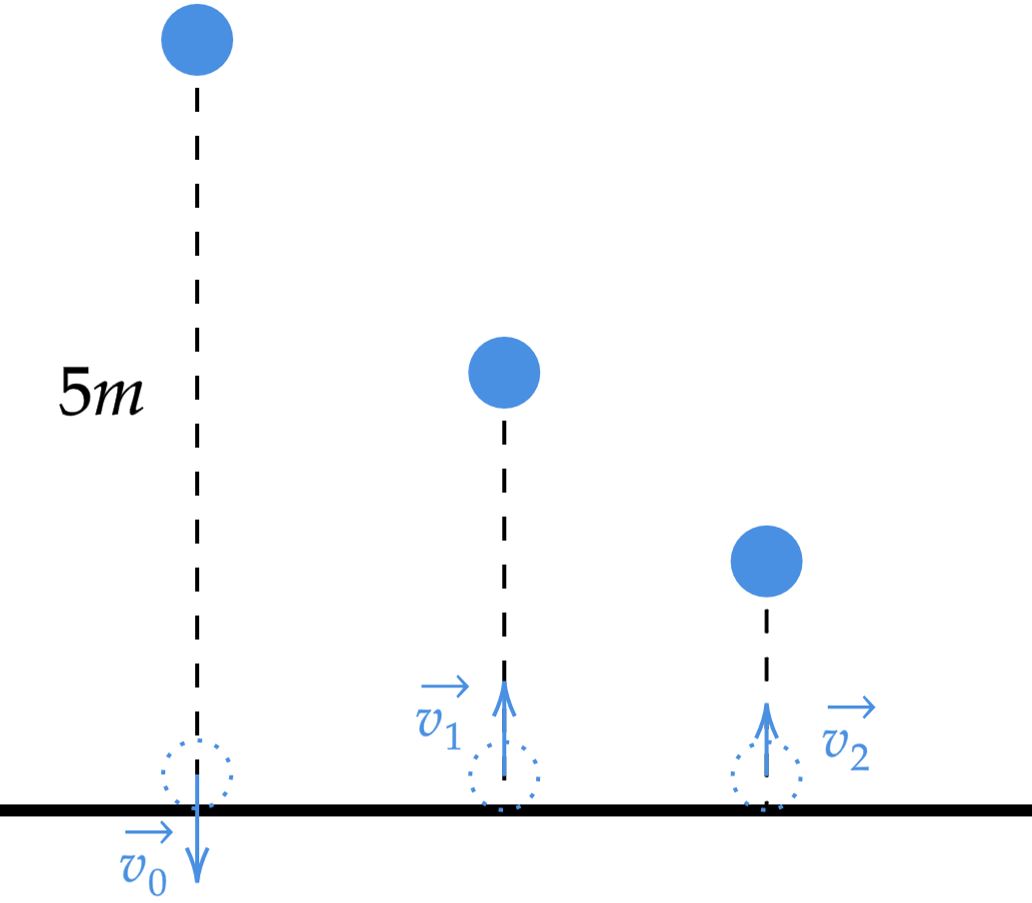Veja que, teremos uma queda a partir do repouso, uma colisão, uma subida até a altura máxima, outra queda, outra colisão, e por fim, outra subida até uma altura máxima. Nesse processo, teremos os intervalos de tempo $t$, $t_1$ e $t_2$, estes que serão o tempo de queda a partir do repouso, o tempo de subida após a colisão - consequentemente o de descida - e o tempo de subida após a segunda colisão, respectivamente. Com conhecimento que o movimento é retilíneo e uniformemente acelerado, têm-se pela lei horária: \begin{matrix} \begin{cases} v_0 = g t \\ v_1 = gt_1 \\ v_2 = gt_2 \end{cases} &\Rightarrow& t+2t_1 + t_2 = {\large{\frac{1}{g}}}(v_0+ 2v_1 + v_2) = 3,24 \ s & \color{royalblue}{(1)} \end{matrix}Como as colisões são parcialmente elásticas, temos: \begin{matrix} e = {\Large{\frac{v_i}{v_{i-1}}}} &\therefore& v_1 = v_0 \cdot e &\wedge& v_2 = v_1 \cdot e \end{matrix}Substituindo os resultados acima em $(1)$: \begin{matrix} {\large{\frac{v_0}{g}}}(1+ 2e + e^2) = 3,24 &,& v_0 \overset{N}{=} g &\because& \underbrace{0 ^2 = (v_0)^2 - 2g(5)}_{\text{cf. Torricelli}} \end{matrix}Continuando,\begin{matrix} e^2 + 2e - 2,24 = 0 &,& e \ge 0 &\therefore& e = 0,8 & \tiny{\blacksquare} \end{matrix} $• \ \text{b)}$ $\color{royalblue}{\text{h = 2,048 m}}$ Vide resultados da questão $(a)$, aplicando a equação de Torriceli: \begin{matrix} 0^2 = (v_2)^2 - 2gh &\Rightarrow& (v_0 \cdot e^2)^2 = 2gh &\therefore& h = 2,048 \ m & \tiny{\blacksquare} \end{matrix}