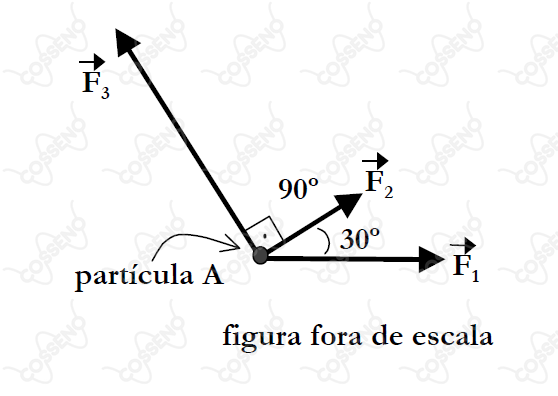
Três forças coplanares , e passam a atuar sobre uma partícula A que, inicialmente, encontrava-se em repouso, conforme a figura abaixo. Para que a partícula fique em equilíbrio, devemos aplicar sobre ela uma quarta força cujo módulo, em newtons, vale
$\sin{30º}$= $\cos{60º} = 0{,}5$
$\sin{60º}$= $\cos{30º} = \frac{\sqrt{3}}{2}$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Apriori realize a decomposição da força $\vec{F_{3}}$ e da força $\vec{F_{2}}$.
Após realizar essa decomposição iremos analisar a força resultante na horizontal e na vertical.
Analisando a horizontal podemos escrever que o módulo da força resultante $\vec{F_{x}}$ na horizontal é igual a :
$F_{x} = |F_{3} \cdot \cos60° - F_{2} \cdot \cos30° - F_{1}| = |16 \cdot 1/2 - 2 \cdot \sqrt{3} \cdot \sqrt{3}/2 - 5|$
$= F_{x} = |8 - 3 - 5| = \boxed{F_{x} = 0}$
Analisando a vertical podemos escrever que o módulo da força resultante $\vec{F_{y}}$ na vertical é igual a :
$F_{y} = |F_{3} \cdot \cos30° + F_{2} \cdot \cos 60°| = 16 \cdot \sqrt{3}/2 + 2\cdot \sqrt{3} \cdot 1/2 $
$\boxed{F_{y} = 9\sqrt{3} \text{ N}}$
Note que a força resultante sobre essa partícula é a força $\vec{F_{y}}$ , para a partícula entrar em equilíbrio a força $\vec{F_{4}}$ deve ter o mesmo módulo de $\vec{F_{y}}$ , mesma direção e sentido oposto a essa força.
$\therefore$
$\boxed{|\vec{F_{4}}|= 9\sqrt{3} \text{ N}} $
$\text{Resposta : Alternativa C}$

