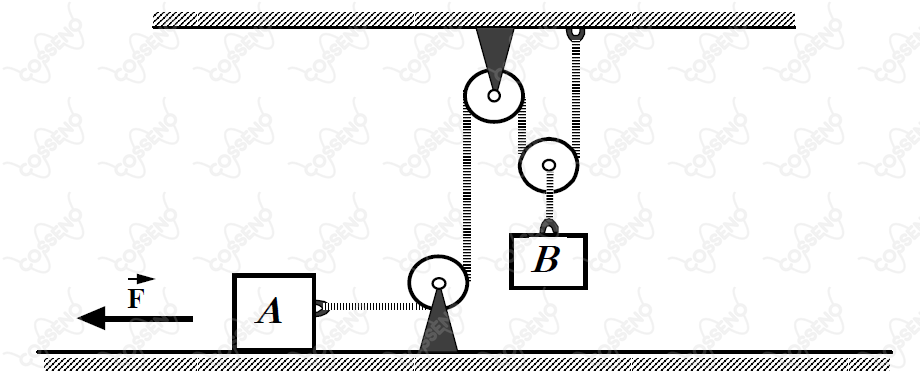
No sistema apresentado na figura abaixo, o fio e as polias são ideais, todos os atritos são desprezíveis e o módulo da força que atua sobre o bloco A vale . Considerando a aceleração da gravidade igual a e sabendo que as massas de A e de B valem e , respectivamente, a aceleração do bloco B, em , é igual a
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A grande ideia aqui é notar que a aceleração do bloco $A$ não será a mesma do bloco $B$. E assim, precisamos de uma equação que as relacione. Tal equação junto às equações vindas da aplicação da segunda lei de Newton nos blocos nos dará o resultado.
Nós chamamos de vínculo geométrico o estudo da relação entre essas acelerações. Na verdade, ele é puramente de natureza cinemática e espacial, e independe da natureza dinâmica. Observe que sempre que o fio em $A$ se desloca de $\Delta x$ esse deslocamento se redistribui igualmente nos dois ramos do fio nos quais a polia está suspensa. Ou seja, na prática, a polia se desloca de um valor $\dfrac{\Delta x}{2}$. Ou seja, para deslocamento de $A$, $B$ se desloca pela metade. Isso nos garante que a aceleração de $B$ é metade da de $A$: $$a_{A} = 2a_{B}$$
Aplicando a segunda lei nos bloco $A$: $$550 - T = 20 \cdot a_{A}$$Em $B$:$$2T-15\cdot 10 = 15\cdot a_{B}$$Observe que a tração em $B$ é $2T$, pois na realidade os dois trechos de fio aplicam tração para cima na polia e essa aplica uma tração dobrada no fio que se liga a $B$. Finalmente, basta resolver esse sistema de três equações para encontrar a aceleração de $B$: $$a_B = 10 \ m/s^2 \Rightarrow Letra \ A$$

