Uma pesquisa foi realizada com um grupo de Cadetes da AFA. Esses Cadetes afirmaram que praticam, pelo menos uma, dentre as modalidades esportivas: voleibol, natação e atletismo. Obteve-se, após a pesquisa, os seguintes resultados:
I) Dos Cadetes que praticam voleibol, não praticam outra modalidade esportiva;
II) Dos Cadetes que praticam natação, não praticam outra modalidade esportiva;
III) Dos Cadetes que praticam atletismo, não praticam outra modalidade esportiva e
IV) Cadetes praticam as três modalidades esportivas.
Marque a alternativa FALSA.
A quantidade de Cadetes que
CossenoGPT
Teste
gratuitamente agora
mesmo! 
Para resolver esse tipo de questão, na maioria das vezes utilizamos o diagrama de Venn (três círculos que se intersectam dois a dois distintamente. Nesse diagrama, temos representada cada parcela das grandezas consideradas.
No nosso caso, iremos fazer o diagrama de Venn com os esportes natação, atletismo e volei, representados por três círculos. Cada círculo completo representa a totalidade de pessoas que praticam aquele esporte (podendo ou não praticar outro esporte também).
A parte dos círculos que não possui interseção com os outros círculos, representa a quantidade de pessoas que pratica exclusivamente aquele esporte. Enquanto a região que pertence aos três círculos simultaneamente ( a partezinha central) representa o número de pessoas que praticam todos os três esportes. Assim, do enunciado, podemos formar o seguinte diagrama:
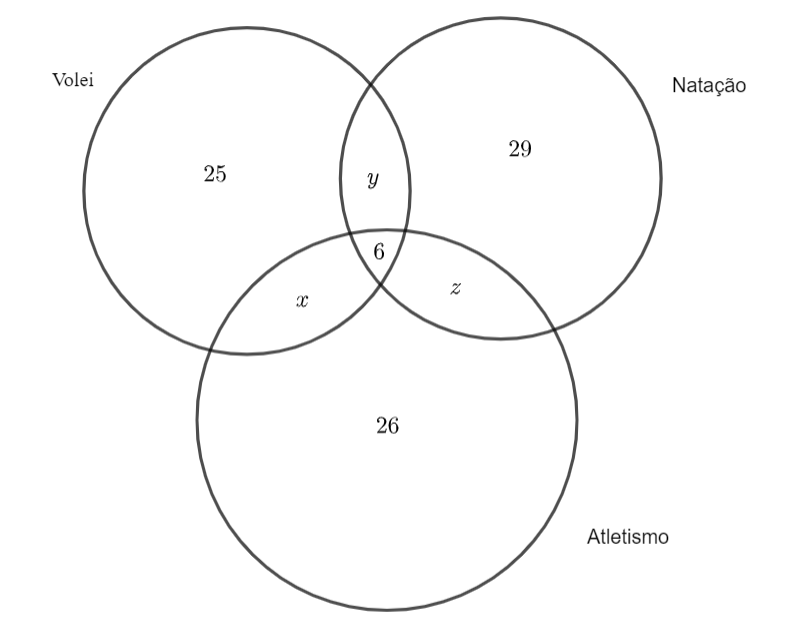Observe que as únicas quantidades de pessoas que não são óbvias, são as pessoas que praticam $2$ e apenas $2$ esportes (representados pelas letras $x, y$ e $z$).
Mas do enunciado: $$\begin{cases} x+y+6+25 = 66 \\ x+z+6+29=68 \\ y+z+6+26=70 \end{cases}$$
Resolvendo, encontramos $x = 15, y = 20, z = 18$.
O total de pessoas pesquisadas é a soma das quantidades de cada região delimitada pelos contornos: $$x + y+ z+25 + 29 + 26 + 6 = 139 < 150 \Rightarrow Letra \ B$$
Ampliar Imagem
