Para avaliar o papel da “Downforce”, considere um carro de Fórmula 1, de massa , realizando uma curva em determinada pista plana. Ao se desprezar completamente os efeitos produzidos pelo seu movimento em relação ao ar, mas considerando o atrito entre pneus e o asfalto, o carro consegue fazer a curva, sem derrapar, a uma velocidade máxima . Porém, ao levar em conta, especificamente, a atuação da “Downforce” (desconsiderando a força de arrasto) a velocidade máxima do carro, nessa mesma curva, muda em função de . Nessas condições, o gráfico que melhor representa a relação em função de é
CossenoGPT
Teste
gratuitamente agora
mesmo! 
Sendo a força de atrito máxima $\mu \cdot F_n$ a resultante centrípeta do carro, que produzirá a velocidade máxima, temos que$$\mu \cdot F_n = M\cdot \dfrac{V^2}{R} \implies V = \sqrt{\dfrac{\mu \cdot F_n \cdot R}{M}~}$$$$\mu \cdot F_n '= M\cdot \dfrac{(V')^2}{R}\implies V' = \sqrt{\dfrac{\mu \cdot F_n' \cdot R}{M}~}$$em que $F_n$ e $F_n' = F_n + D$ são as normais exercidas na pista quando as velocidades são, respectivamente, $V$ e $V'$ ; $\mu$ é o coeficiente de atrito estático entre os pneus e o asfalto; $M$ e $R$ são, respectivamente, a massa do carro e o raio da pista.
Assim, considerando ainda $\dfrac{V'}{V} = g(D)$:$$\dfrac{V'}{V} = \sqrt{\dfrac{F_n'}{F_n}~} = \sqrt{1+\dfrac{D}{F_n}~} \implies g(D) = \sqrt{1+\dfrac{D}{F_n}~}$$
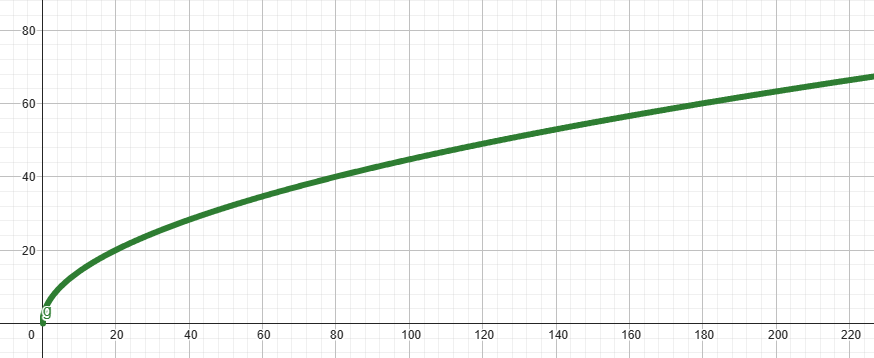O gráfico é melhor representado na $\text{Alternativa } \mathbb{(B)}$
Ampliar Imagem
