Considere duas rampas e , respectivamente de massas e , em forma de quadrantes de circunferência de raios iguais a , apoiadas em um plano horizontal e sem atrito. Duas esferas e se encontram, respectivamente, no topo das rampas e e são abandonadas, do repouso, em um dado instante, conforme figura abaixo.

Quando as esferas perdem contato com as rampas, estas se movimentam conforme os gráficos de suas posições , em metros, em função do tempo , em segundos, abaixo representados.
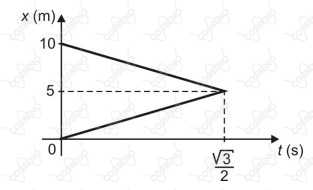
Desprezando qualquer tipo de atrito, a razão das mo massas e das esferas e , respectivamente, é
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Sendo $r$ o raio das rampas, $m_n$ a massa da enésima esfera e $v_n$ a velocidade por ela adquirida, temos que:$$m_ngr = \dfrac{m_nv_n^2}{2} \implies v_n = \sqrt{2gr~}$$Percebamos que a velocidade só depende do raio $r$, que é o mesmo nas duas rampas, ou seja: $v_1 = v_2 = V$.
Há transferência de quantidade de movimento na perda de contato com as rampas e, de acordo com os gráficos apresentados, as velocidades adquiridas por cada rampa são iguais em módulo: $v_A = v_B = V'$ . Isto implica, sabendo que $m_A = 1~\pu{kg}$ e $m_B = 2~\pu{kg}$ são, respectivamente, as massas das rampas $\pu{A}$ e $\pu{B}$, que:$$m_A\cdot v_A = m_1\cdot v_1 \implies \color{red}{1\cdot V' = m_1\cdot V}$$$$m_B\cdot v_B = m_2\cdot v_2 \implies \color{red}{2\cdot V' = m_2\cdot V}$$
Calculando a razão entre as duas relações encontradas, determina-se:$$\boxed{\dfrac{m_1}{m_2} = \dfrac{1}{2}}$$
$$\pu{Alternativa } \mathbb{(A)}$$

21:32 24/07/2024
Não sei se foi isso que quiseram dizer na primeira parte, mas seria Epotencial = Ecinética bola + Ecinética rampa, é não só da bola.

