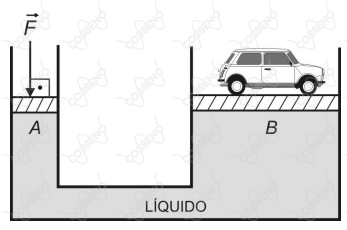
A figura abaixo representa um macaco hidráulico constituído de dois pistões e de raios e , respectivamente. Esse dispositivo será utilizado para elevar a uma altura de , em relação à posição inicial, um veículo de massa igual a tonelada devido à aplicação de uma força . Despreze as massas dos pistões, todos os atritos e considere que o líquido seja incompressível.
Nessas condições, o fator de multiplicação de força deste macaco hidráulico e o trabalho, em joules, realizado pela força , aplicada sobre o pistão de menor área, ao levantar o veículo bem lentamente e com velocidade constante, são, respectivamente,
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Área da seção $A$ : $S_A = \pi \cdot 60^2~\text{cm}^2$
Área da seção $B$ : $S_B = \pi \cdot 240^2~\text{cm}^2$
Pelo Princípio de Pascal, temos que o fator $K$ multiplicador da força é exatamente a constante em que $F$ será multiplicada para que atinja, no pistão B, uma força de pressão de $1~\text{Tf}$ (uma tonelada-força), o mesmo que $10^4~\text{N}$. Este fator é assim calculado: $$\dfrac{F}{S_A} = \dfrac{10^4}{S_B} \implies K = \dfrac{10^4}{F} = \dfrac{\pi}{\pi} \cdot \left(\dfrac{240}{60}\right)^2 \implies \color{red}{\boxed{K = 16}~, ~F = 625~\text{N}}.$$
Ou seja, esse sistema hidráulico tem uma fator $16$ de multiplicador de força.
Em relação ao trabalho realizado por $F$ : em $B$, eleva-se $2~\text{m}$ do líquido num raio $R_B$, portanto o pistão $A$ desloca esse mesmo volume.
Pela conservação de volume, sendo $h$ a distância que $A$ desce:$$S_A \cdot h = S_B \cdot 2 \implies h = 32~\pu{m}$$
Portanto, o trabalho realizado pela força $F$ é$$\color{red}{\boxed{F\cdot h = 2,0 \cdot 10^4~\pu{J}}}$$
$$\text{Alternativa } \mathbb{(C)}$$

