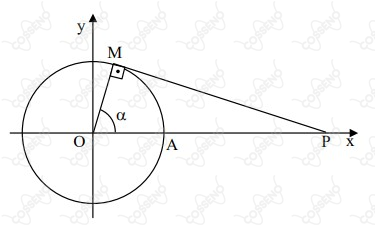
Na figura abaixo, a circunferência de centro é trigonométrica, o arco tem medida é um triângulo retângulo em . Esse triângulo tem por perímetro
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Como a questão nos afirma que a circunferência de centro O é trigonométrica, sabemos que $ \pu{ \overline{OM} = \overline{OA} = 1} $
Sabemos também que:
1) $$ cos(\alpha) = \frac{1}{\overline{OP}} \therefore \overline{OP} = \frac{1}{cos(\alpha)} $$
2) $$ sen(\alpha) = \frac{\overline{MP}}{\overline{OP}} \therefore \overline{MP} = tg(\alpha) $$
Portanto, podemos descobrir no $ \varDelta{OMP} $ o perímetro pedido:
$$ 2p = \overline{OM} + \overline{MP} + \overline{OP} = 1 + \frac{sen(\alpha)}{cos(\alpha)} + \frac{1}{cos(\alpha)} = \frac{sen(\alpha) + cos(\alpha) + 1}{cos(\alpha)} $$
Gabarito Letra A!

15:19 04/04/2023
Perfeito, basta chamar a atenção que o raio da circunferência trigonometrica ( OM = 1 ) é de uma unidade ...

