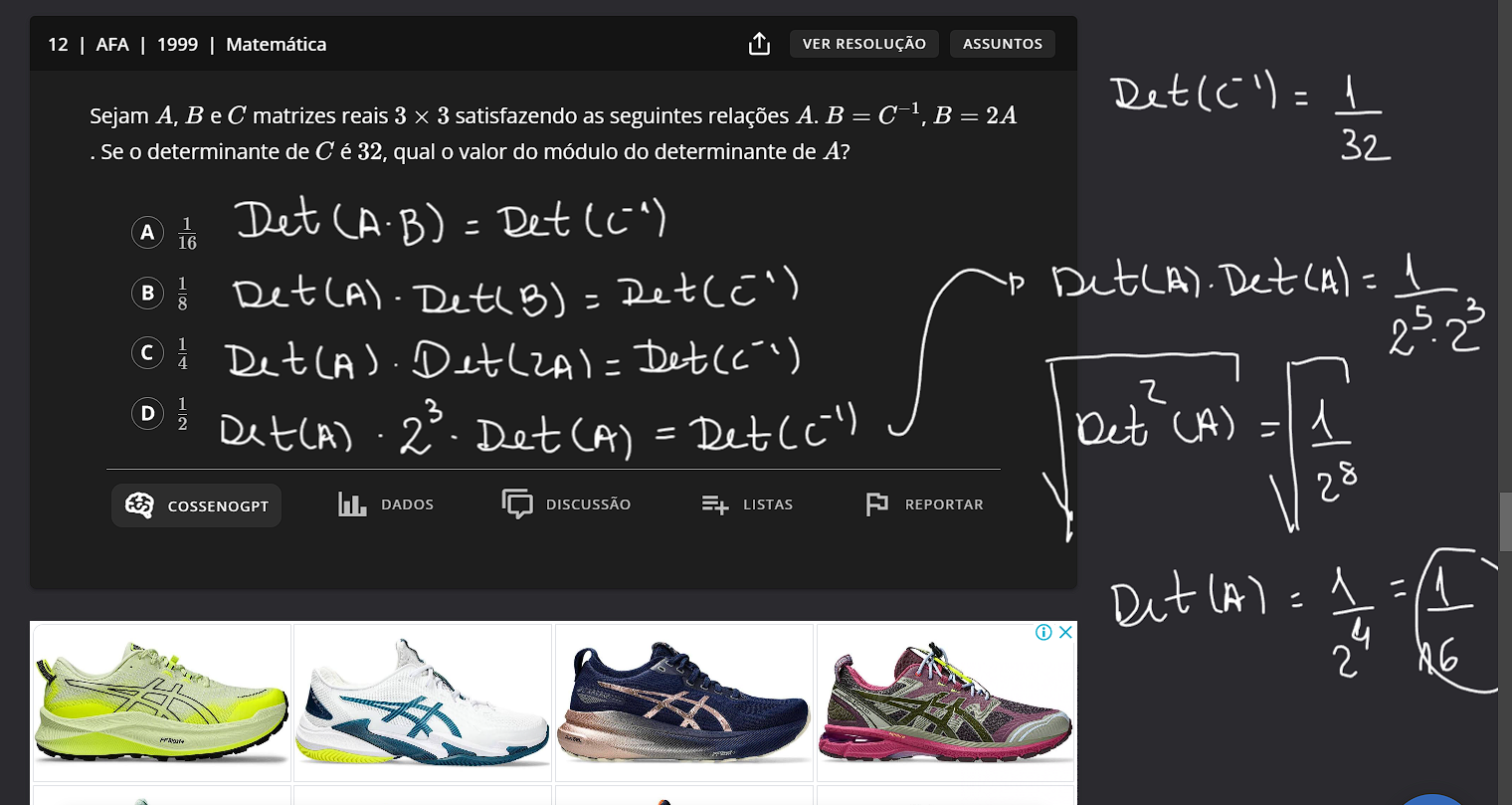
Sejam , e matrizes reais satisfazendo as seguintes relações . , . Se o determinante de é , qual o valor do módulo do determinante de ?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Usando as relações conhecidas, temos que:
1) $ \pu{det(C^{-1})} = \pu{\frac{1}{det(C)}} $.
2) $ \pu{det(\alpha.A)} = \alpha^{ordem}.det{A} $ , em que $ \pu{\alpha} $ é uma constante, e ordem significa a ordem da matriz.
Com base nessas regras, podemos resolver a equação matricial dada:
$$ A.B = C^{-1} \therefore det(A.B) = det(C^{-1}) \implies det(A).det(2A) = \frac{1}{det(C)} \therefore 2^3.[det(A)]^2 = \frac{1}{32} $$
Portanto, temos que: $$ 8.[det(A)]^2 = \frac{1}{32} \implies \left\vert {det(A)} \right\vert = \frac{1}{16} $$
Gabarito Letra A!
Ampliar Imagem


