Observe o gráfico a seguir.
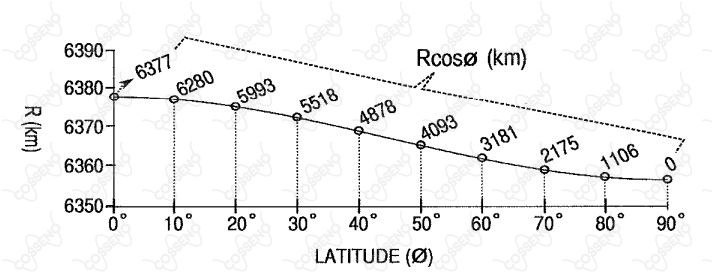
O gráfico da figura acima mostra a variação do raio da Terra () com a latitude (). Observe que foram acrescentadas informações para algumas latitudes, sobre a menor distância entre o eixo da Terra e um ponto na superfície da Terra ao nível do mar, ou seja, . Considerando que a Terra gira com uma velocidade angular , qual é, aproximadamente, a latitude de quando a velocidade de P em relação ao centro da Terra se aproxima numericamente da velocidade do som?
$v_{som}=340 \ m/s$
$\pi=3$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Para calcular a velocidade em determinado ponto, basta fazermos $v = \omega\cdot r$.
Neste caso, o raio $r$ varia conforme a latitude: $r = R\cos\phi$, conforme dado no enunciado.
Já a velocidade angular da terra $\omega$ é constante: todos os pontos levam $\pu{24 h}$ para realizarem uma revolução. Portanto: $$\omega = \omega_T = \dfrac{2\pi}{24}=\dfrac{\pi}{12}\simeq\pu{\dfrac{1}{4} rad/h}$$
Assim, para $v=\pu{340 m/s}$, basta equacionar: $$\begin{align*}\pu{340 m/s} = r\cdot \pu{\dfrac{1}{4} rad/h}\\ 340 = r\cdot \dfrac{1}{4\cdot 3600}\\ r=\pu{4896 km}\end{align*}$$
No gráfico, podemos ver que isso ocorre com $\boxed{\phi\simeq40º}$ (Gabarito C)
Se quiséssemos um valor mais preciso, bastaria fazer $$r = R\cos\phi\\ 4896 = 6370\cdot\cos\phi\\ \phi=\arccos\dfrac{4896}{6370}\simeq 39{,}8º$$

