Observe a figura a seguir.
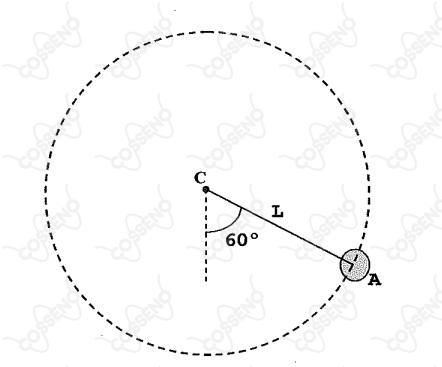
A figura acima mostra uma esfera presa à extremidade de um fio ideal de comprimento , que tem sua outra extremidade presa ao ponto fixo . A esfera possui velocidade no ponto quando o fio faz um ângulo de com a vertical. Sendo ainda, igual a velocidade mínima que a esfera deve ter no ponto , para percorrer uma trajetória circular de raio , no plano vertical, e sendo , o ponto da trajetória onde a esfera tem velocidade de menor módulo, qual é a razão entre as velocidades nos pontos e , ?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

O ponto B encontra-se no topo da trajetória circular.
Conservação da Energia Mecânica:
$$\frac{m.v²{\tiny a}}{2}+mgL(1-cos60°)=mg2L+\frac{m.v²{\tiny b}}{2}$$
$$v²{\tiny a}=3gL + v²{\tiny b}$$
Temos que a resultante centrípeta no topo da curva é:
$$\frac{m.v²{\tiny b}}{L}=mg$$
$$v²{\tiny b}=gL$$
Logo:
$$v²{\tiny a}=4gL$$
$$\frac{v{\tiny b}}{v{\tiny a}}=\frac{1}{2}$$

