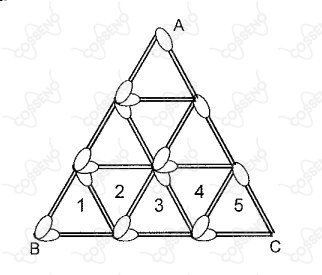
Um grande triângulo equilátero será construído com palitos de fósforos, a partir de pequenos triângulos equiláteros congruentes e dispostos em linhas. Por exemplo, a figura abaixo descreve um triângulo equilátero construído com três linhas de pequenos triângulos equiláteros congruentes (a linha da base do triângulo possui pequenos triângulos equiláteros congruentes).
Conforme o processo descrito, para que seja construído um triângulo grande, com linha de base contendo pequenos triângulos equiláteros congruentes, é necessário, um total de palitos igual a
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Note:
$1°Linha$ de $\Delta$ - $3$ palitos
$2°Linha$ de $\Delta$ - $3+6$ palitos
$3°Linha$ de $\Delta$ - $3+6+9$ palitos
Pela figura podemos perceber que a quantidade de palitos trata-se de uma soma de $PA$ de primeiro termo $3$ e razão $3$. Porém, note que a quantidade de triângulos nas linhas está em PA, com primeiro termo $1$ e razão $2$. Como as duas $PA$ estão relacionadas, temos:
Quantidade de linhas de triângulos:
$$201=1+(n-1)*2$$
$$n=101$$
Assim a soma dá-se por:
$$S=3*(1+2+3+4+...+101)$$
$$S=3*\frac{(1+101)101}{2}$$
$$S=15453$$

