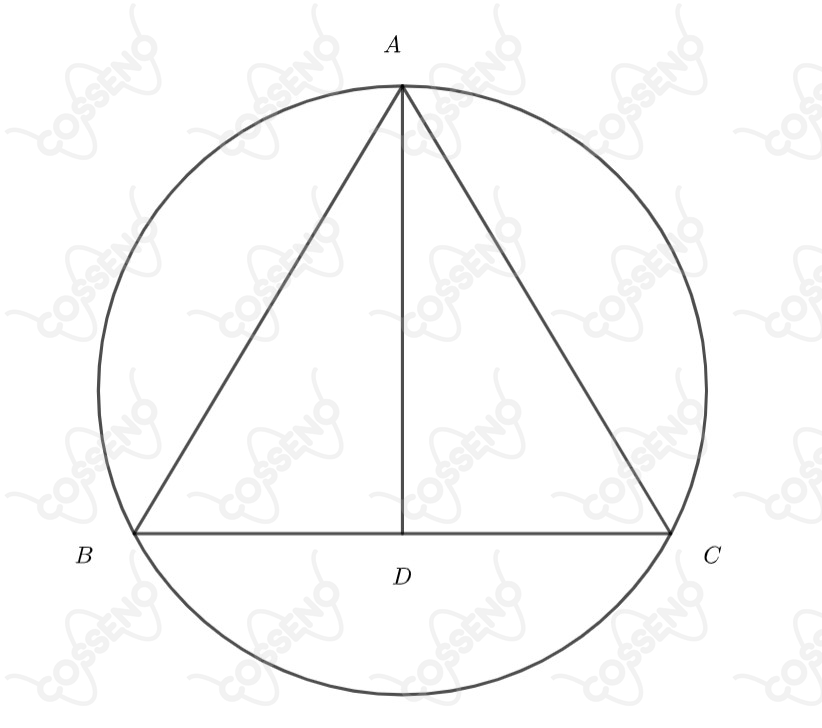
Considere o triângulo isósceles inscrito em um círculo, conforme figura abaixo. Suponha que o raio do círculo cresce a uma taxa de e a altura do triângulo cresce a uma taxa de . A taxa de crescimento da área do triângulo no instante em que o raio e a altura medem, respectivamente, e , é
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Seja $AD=h$ e $BD=DC=a$
No triangulo retângulo $BDO$ sendo $O$ o centro da circunferência, temos: $$r² =(h-r)² + a² $$ $$a=\sqrt{2hr-h²} $$
A área do Triângulo $ABC$ é dada por: $$Área=\frac{h(2a)}{2}=ha$$
Derivando em relação ao tempo e aplicando a regra do produto, temos: $$Taxa = \frac{dh}{dt}a + h\frac{da}{dt}$$
Para terminarmos, temos que achar $\frac{da}{dt}$, assim, derivando $a$, temos: $$\frac{da}{dt} = \frac{1}{2}\frac{1}{\sqrt{2hr-h²}}(2\frac{dh}{dt}r+2h\frac{dr}{dt} - 2h\frac{dh}{dt})$$
Como $\frac{dh}{dt}=5$ e $\frac{dr}{dt}=3$, $r=10$ e $h=16$, fica: $$\frac{da}{dt}= \frac{1}{\sqrt{64}}(5*10+16*3-16*5)$$
$$\frac{da}{dt}=\frac{18}{8}=\frac{9}{4}$$
Pelo Pitágoras sabemos que o valor de $a$ nesse instante é $8$, completando temos: $$Taxa = 5*8+16*\frac{9}{4}$$ $$Taxa=40+36=76$$

