Considere um recipiente, sobre uma plataforma, sujeito à pressão atmosférica . Esse recipiente contém um volume inicial de um gás monoatômico ideal em equilíbrio e tem um êmbolo de seção transversal de área e de massa . Para monitorar a aceleração do sistema, a plataforma foi suspensa por um dinamômetro, como ilustrado na figura. Por causa de uma ação de uma força externa vertical, o êmbolo atinge uma nova posição de equilíbrio. Nessa posição a leitura do dinamômetro indica que a aceleração do sistema é de de para cima.
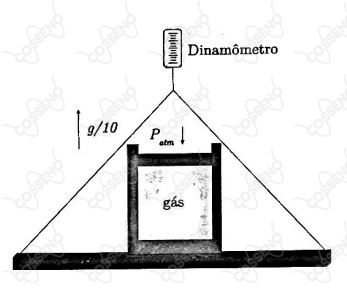
Determine o módulo do deslocamento do êmbolo, com relação ao fundo do recipiente, considerando que a transformação do gás é isentrópica.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

i) no êmbolo em equilíbrio, adotando sentido positivo para cima, teremos:
$p_{1}.A = mg + P_{atm} \therefore \boxed{p_{1} = \frac{mg}{a} + P_{atm}}$
ii) no êmbolo acelerado, teremos:
$p_{2} - P_{atm}.A - mg = \frac{1}{10}mg \therefore \boxed{p_{2} = \frac{11mg}{10A} + P_{atm}}$
iii) aplicando a equação de poisson para transformações adiabáticas, lembrando que para gases monoatômicos, $\gamma = \frac{5}{3}$:
$p_{1}.V_{i}^{\gamma} = p_{2}.V_{2}^{\gamma}$
$V_{2} = V_{i}(\frac{p_{1}}{p_{2}})^\frac{1}{\gamma}$
$\boxed{V_{2} = V_{i}(\frac{mg + P_{atm}.A}{1,1mg + P_{atm}.A})^\frac{3}{5}}$
iv) finalmente, calculando o $\Delta x$:
$\Delta x.A = V_{1} - V{2}$
$\therefore \boxed{\Delta x = \frac{V_{i}}{A}.[1 - (\frac{mg + P_{atm}.A}{1,1mg + P_{atm}.A})^\frac{3}{5}]}$

