Considere duas partículas de massa , cada qual presa numa das pontas de uma corda, de comprimento e massa desprezível, que atravessa um orifício de uma mesa horizontal lisa. Conforme mostra a figura, a partícula sobre a mesa descreve um movimento circular uniforme de raio e velocidade angular . A partícula suspensa também descreve esse mesmo tipo de movimento, mas com velocidade angular , estando presa a uma mola de constante elástica e comprimento natural desprezível, mantida na horizontal.
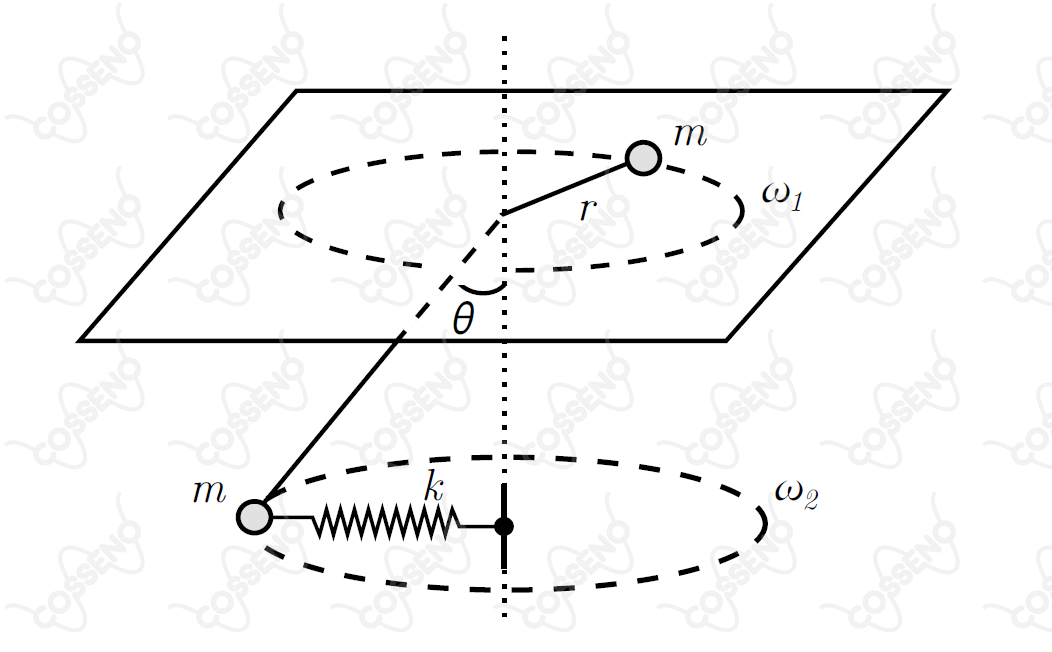
Sendo o módulo da aceleração da gravidade e o ângulo do trecho suspenso da corda com a vertical, a razão é dada por
CossenoGPT
Teste
gratuitamente agora
mesmo! 

i) Nomeando o raio de rotação da partícula de baixo de $R$, teremos:$$sen(\theta) = \frac{R}{(l-r)} \therefore R = (l-r)sen(\theta)$$
ii) Na parte de cima, observamos que a tração é a resultante centrípeta $$T = Rcp \therefore T = m\omega_{1}^2r$$
iii) Na parte de baixo, decompondo a força de tração, teremos que:$$T\cos(\theta) = mg \therefore T = \frac{mg}{\cos(\theta)}$$$$T\sin(\theta) + Fel = Rcp \\ \frac{mg}{\cos(\theta)}\cdot \sin(\theta) + kR = m\omega_{2}^2R \\ \frac{mg}{\cos(\theta)}\cdot \sin(\theta) + k\cdot (l-r)\sin(\theta) = m\omega_{2}^2(l-r)\sin(\theta)\\ \omega_{2}^2 = \frac{g}{(l-r)\cos(\theta)} + \frac{k}{m}$$
iv) $$\frac{mg}{\cos(\theta)} = m\omega_{1}^2r \therefore \omega_{1}^2 = \frac{g}{r\cdot cos(\theta)}$$
v) $$\left(\frac{\omega_{2}}{\omega_{1}}\right)^2 = \boxed{\frac{r(mg + k(l-r)\cdot\cos(\theta))}{mg(l-r)}}$$

