Uma prancha homogênea de massa é sustentada por dois roletes, interdistantes de , que giram rapidamente em sentidos opostos, conforme a figura.
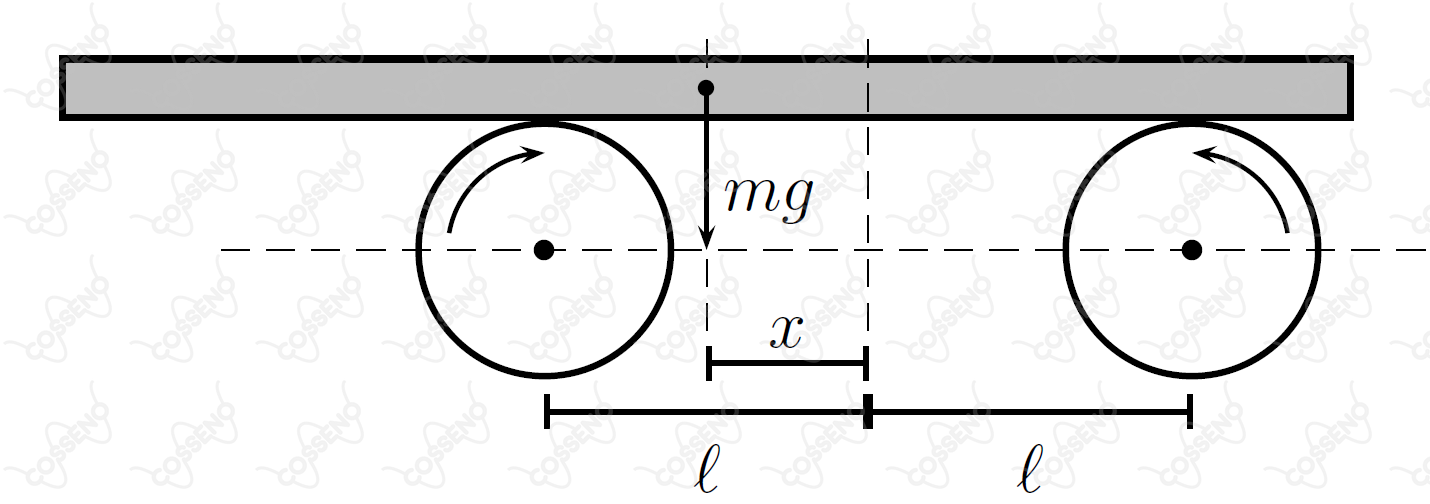
Inicialmente o centro de massa da prancha dista da linha intermediária entre os roletes. Sendo o coeficiente de atrito cinético entre os roletes e a prancha, determine a posição do centro de massa da prancha em função do tempo.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

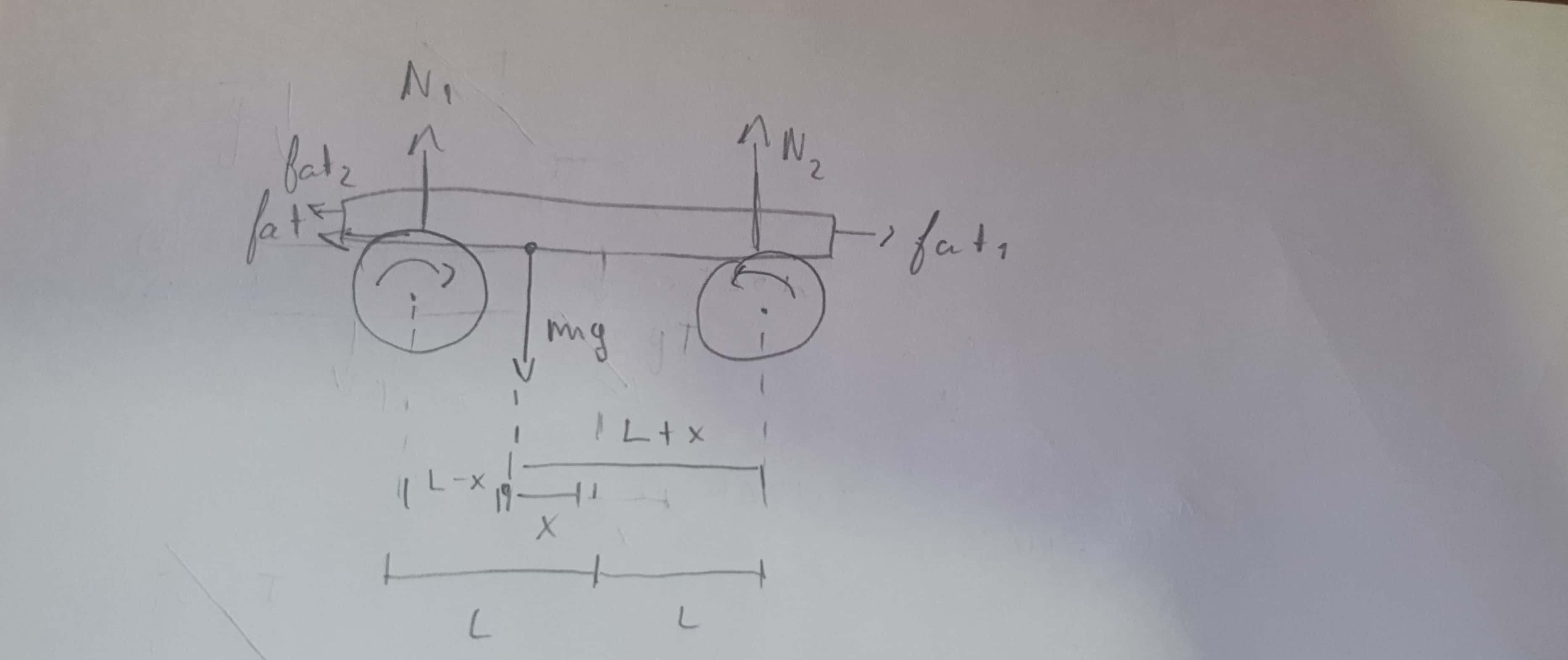
Primeiramente, analisaremos as forças presentes no sistema, disso resulta: $$ N1 + N2 = mg ( I ) $$
$$ N1 (L-x) = N2 (L+x)( II ) $$
$$ fat1 - fat2 = ma (III) $$
Sabe-se que:
$$ fat = N.\mu $$
Logo, manipulando algebricamente a equação III tem-se:
$$ (N1-N2)L = (N1+N2)x $$
Substituindo I e II em III
$$(ma/\mu) = mgx $$
$$ maL/\mu = mgx $$
$$ a = gx\mu/L ( IV ) $$
A equação IV caracteriza um MHS, onde podemos utilizar a relação
$$ a = \omega² L $$
Assim
$$ \omega = \sqrt {g\mu/L} $$
Utilizando agora a função horária do MHS
$$ x(t) = xcos(\omega t) $$
$$ x(t) = xcos(t \sqrt {g\mu/L} ) $$

Ampliar Imagem

